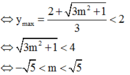Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y = x 2 − 2 x + m trên đoạn [-1;2] bằng 5.
A. 3
B. 1
C. 2
D. 4
a) Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\) có bao nhiêu giá trị nguyên của tham số \(a\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
b) Tìm tất cả các giá trị của tham số m để hệ bất pt \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\) có nghiệm
c) Gọi (x;y) là nghiệm của hệ bất pt \(\left\{{}\begin{matrix}x-2y-2\le0\\4x-3y+12\ge0\\x+3y+3\ge0\\2x+y-4\le0\end{matrix}\right.\). Tìm giá trị lớn nhất của biểu thức F=4x+5y-6
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
Có tất cả bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y = x 2 - 2 x + m trên đoạn - 1 ; 2 bằng 5.
A. 3
B. 1
C. 2
D. 4
Có tất cả bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y = x 2 - 2 x + m trên đoạn - 1 ; 2 bằng 5.
A. 3
B. 1
C. 2
D. 4
Chọn C.
Phương pháp: Biện luận theo m.
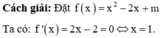

Cho hàm số y= 2x^2 -3(m+1)x +m^2 +3m -2 , m là tham số . TÌm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
cho hàm số y=x^2-3(m+1)x+m^2+3m-2, m là tham số . Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Có bao nhiêu giá trị thực của tham số m để hàm số y = cos x + m . sin x + 1 cos x + 2 có giá trị lớn nhất bằng 1
A. 0
B. 1
C. 2
D. 3
Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y=|x^2+2x+m-4| trên đoạn [-2;-1] bằng 4
Cho hàm số \(y=-2x^3+(2m-1)x^2-(m^2-1)x+2\). Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
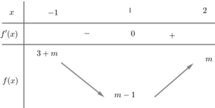
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y = m sin x + 1 cos x + 2 nhỏ hơn 2?
A. 5
B. 3
C. 4
D. 6
Đáp án A
Giả sử giá trị lớn nhất của hàm số là M. Khi đó
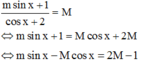
có nghiệm
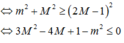
xét ![]()
Có ![]()
Suy ra ![]() có 2 nghiệm phân biệt
có 2 nghiệm phân biệt
![]()
Ta có
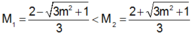
suy ra 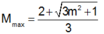
Yêu cầu bài toán