Cho tứ giác ABCD trong đó có A ^ = 60 0 , C ^ = 150 0 , D ^ = 75 0 . Tính số đo của góc B ^ ?
PB
Những câu hỏi liên quan
1 Cho tứ giác ABCD, trong đó có A +B = 140°. Tổng C + D = A. 220° B. 200° C. 160° D. 150°
tứ giác ABCD có tọa độ các đỉnh như sau A(0:2) , B(3:0) , C(0:-2) , D(-3:0) . tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.
Tứ giác ABCD có góc C bằng 600; góc D bằng 600 . Gọi E là giao điểm của các đường phân giác trong của góc A và góc B. Số đo của góc AEB là …0.
Cho tứ giác ABCD có góc A 70 độ, góc D 80 độ và góc ngoài ở đỉnh C 60 độ.
a Tính góc B của tứ giác ABCD
b Chứng minh rằng tổng 2 đường chéo luôn lớn hơn tổng 2 cạnh đối của tứ giác đó.
Tứ giác ABCD có tọa độ các đỉnh như sau A(0;2); B(3; 0); C(0;-2) ; D(-3;0).Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.
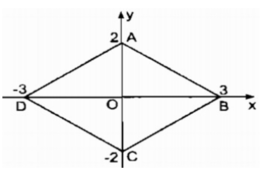
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13
Đúng 0
Bình luận (0)
1cho tứ giác ABCD có 2 đương chéo vuông góc với nhau tại trung điểm O của chúng.CM
a/ tam giác ABC= tam giác ADC
b/ tính các góc của tứ giác ABCD biet rằng Góc ABO= 2BAO VÁ Góc C = 600
2. cho tu giac ABCD co diem O ở trong tứ giác gọi chu vi là 2p. CMR p<OA+OB+OC+OD<3p
Có : \(AB< OA+OB;BC< OB+OC;CD< OC+OD;DA< OD+OA\)
\(P_{ABCD}=2p=AB+BC+CD+DA< 2\left(OA+OB+OC+OD\right)\)
\(\Leftrightarrow\)\(p< OA+OB+OC+OD\)
Lại có : \(OA< AB-OB;OB< BC-OC;OC< CD-OD;OD< DA-OA\)
Cộng vế theo vế từng bđt trên ta được :
\(OA+OB+OC+OD< AB+BC+CD+DA-\left(OA+OB+OC+OD\right)\)
\(\Leftrightarrow\)\(2\left(OA+OB+OC+OD\right)< AB+BC+CD+DA\) (*)
Có tiếp -,- :
\(OA< AB+OB;OA< DA+OD\)\(\Rightarrow\)\(2OA< AB+DA+OB+OD\)
\(OB< AB+OA;OB< BC+OC\)\(\Rightarrow\)\(2OB< AB+BC+OA+OC\)
\(OC< BC+OB;OC< CD+OD\)\(\Rightarrow\)\(2OC< BC+CD+OB+OD\)
\(OD< CD+OC;OD< DA+OA\)\(\Rightarrow\)\(2OD< CD+DA+OC+OA\)
\(\Rightarrow\)\(2\left(OA+OB+OC+OD\right)< 2\left(AB+BC+CD+DA\right)+2\left(OA+OB+OC+OD\right)\)
\(< 2\left(AB+BC+CD+DA\right)+\left(AB+BC+CD+DA\right)\) ( kết hợp với (*) )
\(\Rightarrow\)\(2\left(OA+OB+OC+OD\right)< 3\left(AB+BC+CD+DA\right)\)
\(\Leftrightarrow\)\(OA+OB+OC+OD< 3.\frac{AB+BC+CD+DA}{2}=3.\frac{2p}{2}=3p\)
Vậy \(p< OA+OB+OC+OD< 3p\)
Đúng 0
Bình luận (0)
1/cho tứ giá lồi ABCD có AB=BC=CD=a , \(\widehat{BAD}=75^o,\widehat{ADC}=45^o\).tính AD
2/cho tứ giác ABCD có\(AB-6\sqrt{3},CD=12,\widehat{A}=60^o,\widehat{B}=150^o,\widehat{D}=90^o\). tính BC
Cho tứ giác ABCD có góc A 70 độ, góc D 80 độ và góc ngoài ở đỉnh C 60 độ.
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng 2 đường chéo luôn lớn hơn tổng 2 cạnh đối của tứ giác đó.
cho tứ giác ABCD với goc D =90 do; A=60 do; B = 150 do; CD=12cm. AB là cạnh hionhf vuông có S = 108cm^2. Miền trong tứ giác có điểm M sao cho ABCM là hình bình hành. MH vuông DC
a) CM MC là phân giác BCD
b) DMC là tam giác vuông tại M
c) tam giác AMD cân
d) Tính AD,BC=> Tam giác ADB đều
1) Cho tứ giác ABCD có góc B 1200 , góc C 600, D 900. Tính góc A và góc ngoài đỉnh A2) Cho tứ giác ABCD có phân giác trong của góc A và góc B cắt nhau tại E, phân giác ngoài của góc A và góc B cắt nhau tại F. Chứng minh: AEB frac{C+D}{2}và AFB frac{A+B}{2}Ai giải nhanh nhất trong vong 30 thì mik sẽ like + sao cho nha đang cần gấp giúp mik vs
Đọc tiếp
1) Cho tứ giác ABCD có góc B = 1200 , góc C = 600, D = 900. Tính góc A và góc ngoài đỉnh A
2) Cho tứ giác ABCD có phân giác trong của góc A và góc B cắt nhau tại E, phân giác ngoài của góc A và góc B cắt nhau tại F. Chứng minh: AEB = \(\frac{C+D}{2}\)và AFB = \(\frac{A+B}{2}\)
Ai giải nhanh nhất trong vong 30' thì mik sẽ like + sao cho nha đang cần gấp giúp mik vs


