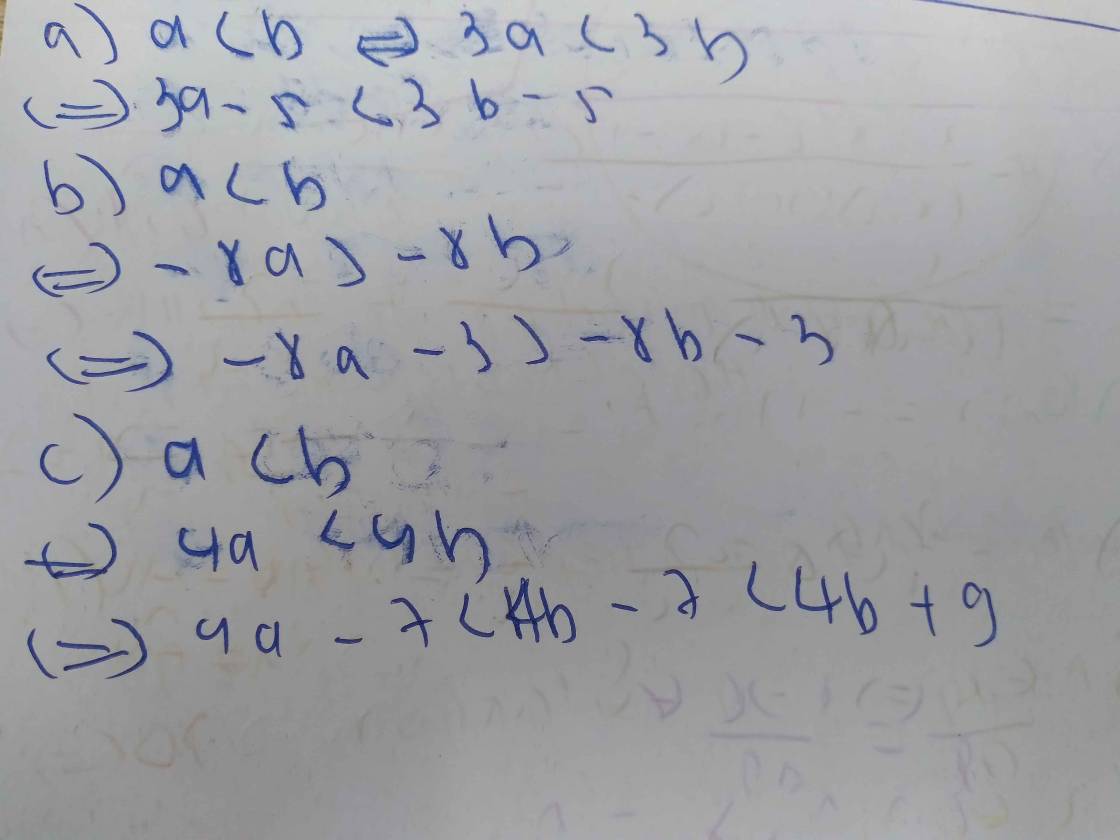ta có:a<b

\(\Rightarrow\)-4a>-4b

\(\Rightarrow\)2-4a>2-4b(1)

ta có: 2<3  \(\Rightarrow\)2-4b<3-ab(2)

(1)(2)suy ra 2-4a>3-4b

a)

`a<b`

`<=>3a<3b`

`<=>3a-5<3b-5`

b)

`a<b`

`<=>-8a> -8b`

`<=>-8a-3> -8b-3`

c)

`a<b`

`<=>4a<4b`

`<=>4a+9<4b+9`

mà `4a-7<4a+9`

`<=>4a-7<4b+9`

Cách làm như trên là không sai, tuy nhiên để chặt chẽ hơn bạn có thể làm như thế này:

Ta có:\(\left\{{}\begin{matrix}4a>4b\\-2>-3\end{matrix}\right.\), cộng 2 vế của bất phương trình ta được \(4a-2>4b-3\left(ĐPCM\right)\)

a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)

Mặt khác: 3b + 5 > 3b + 2 (2)

Từ (1) và (2) suy ra: 3a + 5 > 3b + 2

b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)

Mặt khác: 2 – 4a < 3 – 4a (2)

Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b

a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)

Mặt khác: 3b + 5 > 3b + 2 (2)

Từ (1) và (2) suy ra: 3a + 5 > 3b + 2

b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)

Mặt khác: 2 – 4a < 3 – 4a (2)

Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b

Lời giải:

Xét hiệu $3-4b-(2-4a)=1+4(a-b)>0$ do $1>0$ và $4(a-b)>0$ khi $a>b$

$\Rightarrow 3-4b> 2-4a$ (đpcm)

Ta có: a>b

nên -4a<-4b

\(\Leftrightarrow-4a+2< -4b+2\)

mà -4b+2<-4b+3

nên -4a+2<-4b+3(đpcm)

a) Ta có: a>b => 2a > 2b  (nhân 2 vế với 2)

                     => 2a - 3 > 2b - 3 (cộng 2 vế với -3)

b) Ta có: -4a+1 < -4b+ 1 => -4a < -4b ( cộng 2 vế với -1)

                                       => a > b (nhân 2 vế với -1/4)

c) Ta có: 3-4a < 5c+2 => 3-4a-3 < 5c+2-3 (cộng 2 vế với -3)

                                  => -4a < 5c-1

Mà 5c-1 < -4b nên -4a < -4b => a > b (nhân cả 2 vế với -1/4)

Ta có: \(a>b\Leftrightarrow4a>4b\left(1\right)\) và \(-2>-3\left(2\right)\)

Cộng the từng vế của 2 bất pt: \(\Rightarrow4a-2>4b-3\)