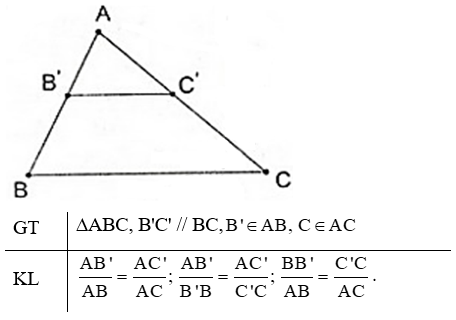
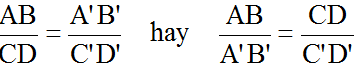Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet đảo.
PB
Những câu hỏi liên quan
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet trong tam giác.
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
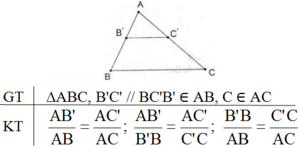
Đúng 0
Bình luận (0)
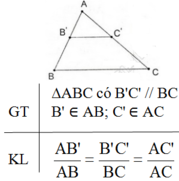
Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Talet.
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
Đúng 0
Bình luận (0)
1. Phát biểu, vẽ hình, ghi giả thiết - kết luận của định lí Ta-let, định lí đảo, hệ quả
2. Phát biểu, vẽ hình, ghi giả thiết - kết luận của tính chất đường phân giác trong tam giác
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - lét đảo ?
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Đúng 0
Bình luận (0)
gt: DE giao AB={ D}, DE giao ={ E}
\(\frac{AD}{AB}\)= \(\frac{AE}{AC}\)
kl: =) DE// BC
Đúng 0
Bình luận (0)
Định lý Ta - lét đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Vẽ hình và Giả thuyết, Kết luận:

GT: △ABC,\(\frac{AM}{AB}=\frac{AN}{AC},\frac{MB}{AB}=\frac{NC}{AC},\frac{AM}{MB}=\frac{AN}{NC}\)
KL: MN // BC
Đúng 0
Bình luận (0)
Câu 1: Phát biểu định lí Talet thuận, đảo. Giả thiết, kết luận, vẽ hình
Câu 2: Phát biểu định lí đảo và hệ quả của định lí Talet. Vẽ hình, viết giả thiết, kết luận
Câu 1:
*Định lí Ta - lét thuận: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Câu 2:
*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.

Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - lét trong tam giác ?
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Đúng 1
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta - lét ?
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:
Đúng 0
Bình luận (0)
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
Đúng 0
Bình luận (0)
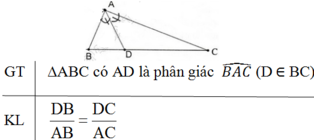
Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận).
Định lý:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Đúng 0
Bình luận (0)
2 : Phát biểu tính chất : " Hai tia phân giác của 2 góc kề bù tạo thành góc vuông " thành định lí dạng : Nếu.... thì
rồi vẽ hình và ghi Giả thiết , kết luận của định lí
Chứng minh định lí và phát biểu
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
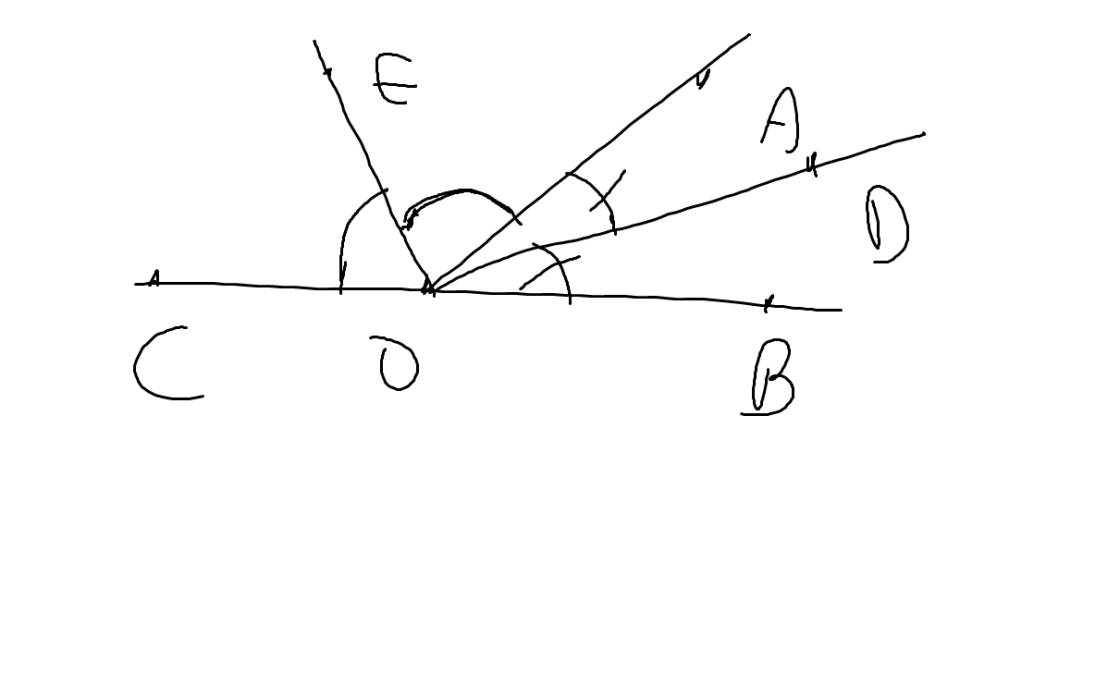
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
Đúng 5
Bình luận (0)