Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
PB
Những câu hỏi liên quan
Trên mặt phẳng tọa độ Oxy cho bốn điểm A, B, C, D có tọa độ nguyên như sau:
A(4;5) B(1;-1) C(4;-4) D(7; -1).
Viết phương trình của các đường thẳng AB, BC, CD và DA.
Phương trình của đường thẳng AB có dạng: y = ax + b.
Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:
5 = a.4 + b (1)
-1 = a.1 + b (2)
Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.
Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.
Vậy phương trình đường thẳng AB là: y = 2x – 3.
Làm tương tự như trên, ta có:
Phương trình đường thẳng BC là: y = -x.
Phương trình đường thẳng CD là: y = x – 8.
Phương trình đường thẳng DA là: y = -2x + 13.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho bốn điểm A, B, C, D có tọa độ nguyên như sau:
A(4;5) B(1;-1) C(4;-4) D(7; -1).
Tính (theo độ, phút) các góc của tứ giác ABCD bằng máy tính bỏ túi.
Hai đường chéo AC và BD vuông góc với nhau tại I.
- Đường thẳng AB có hệ số góc bằng 2, do đó ta có
tgα = 2 ⇒ α = 63 ° 26 ' (tính trên máy tính bỏ túi).
Suy ra ∠ (ABD) ≈ 63 ° 26 '
Tam giác ABD cân, nên cũng có ∠ (ADB) ≈ 63 ° 26 '
Từ đó suy ra ∠ (BAD) = 180 ° - 2. 63 ° 26 ' ≈ 53 ° 8 '
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho bốn điểm A( 7; -3); B( 8; 4); C ( 1; 5) và D(0; -2). Khẳng định nào sau đây đúng? A.
A
C
→
⊥
C
B
→
.
B. Tam giác ABC đều. C. Tứ giác ABCD là hình vuông. D. Tứ giác ABCD không nội tiếp đường tròn.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho bốn điểm A( 7; -3); B( 8; 4); C ( 1; 5) và D(0; -2). Khẳng định nào sau đây đúng?
A. A C → ⊥ C B → .
B. Tam giác ABC đều.
C. Tứ giác ABCD là hình vuông.
D. Tứ giác ABCD không nội tiếp đường tròn.
Ta có
A B → = 1 ; 7 ⇒ A B = 1 2 + 7 2 = 5 2 B C → = − 7 ; 1 ⇒ B C = 5 2 C D → = − 1 ; − 7 ⇒ C D = 5 2 D A → = 7 ; − 1 ⇒ D A = 5 2 ⇒ A B = B C = C D = D A = 5 2 .
Lại có: A B → . B C → = 1 − 7 + 7.1 = 0 nên A B ⊥ B C .
Từ đó suy ra ABCD là hình vuông.
Chọn C.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho bốn điểm :
A(7; -3); B(8; 4); C(1; 5); D(0;-2).
Chứng minh rằng tứ giác ABCD là hình vuông.
Ta có: = (1; 7);
= (1; 7)
=
=> ABCD là hình bình hành (1)
ta lại có : AB2 = 50 => AB = 5 √2
AD2 = 50 => AD = 5 √2
AB = AD, kết hợp với (1) => ABCD là hình thoi (2)
Mặt khác = (1; 7);
= (-7; 1)
1.7 + (-7).1 = 0 => ⊥
(3)
Kết hợp (2) và (3) suy ra ABCD là hình vuông
Đúng 1
Bình luận (2)
trên mặt phẳng tọa độ oxy cho A (5;-3) B(2;4) C(1;5) .tìm tọa độ điểm D sao cho ABCD là hình bình hành
\(\overrightarrow{AB}=\left(-3;7\right)\)
\(\overrightarrow{DC}=\left(1-x_D;5-y_D\right)\)
Để ABCD là hbh thì
\(\left\{{}\begin{matrix}1-x_D=-3\\5-y_D=7\end{matrix}\right.\Leftrightarrow D\left(2;-2\right)\)
Đúng 1
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(1; 2); N(3; – 5); P(5; 7). Tọa độ đỉnh A là:
A. A(7; 9)
B. A(– 2; 0)
C. A(7; – 2)
D. A(7; 0)
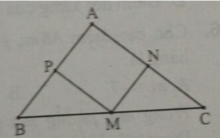
Tam giác ABC có M; N ; P lần lượt là trung điểm của BC; AC ; BC nên PM và MN là đường trung bình của tam giác ABC.
Suy ra: PM// AC; NM // AB.
Do đó, tứ giác ANMP là hình bình hành.
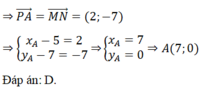
Đúng 0
Bình luận (0)
trong mặt phẳng hệ tọa độ oxy,cho điểm A(2;5)B(0;-7).tọa độ diểm M của AB là
Lời giải:
Tọa độ trung điểm $M$ của $AB$ là:
\(\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}\right)=\left(\frac{2+0}{2}; \frac{5+(-7)}{2}\right)=(1;-1)\)
Đúng 0
Bình luận (2)
Trên mặt phẳng tọa độ Oxy, cho điểm A( 5; 6). Xác định vị trí tương đối của đường tròn (A; 5) với các trục tọa độ?
A. Đường tròn tiếp xúc trục Oy.
B. Đường tròn tiếp xúc với trục Ox.
C. Đường tròn không cắt trục Ox.
D. Đường tròn không cắt trục Oy.
Đáp án A
Ta có khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
Do đó, đường tròn (A; R) tiếp xúc với trục Oy.
Đúng 0
Bình luận (0)
trên mặt phẳng tọa độ Oxy, vẽ điểm A có tọa độ (3;5) tính khoảng cách từ điểm A tới gốc tọa độ


