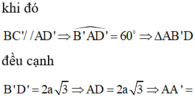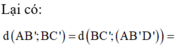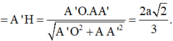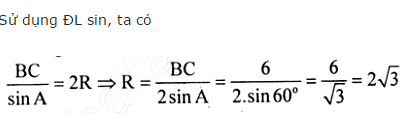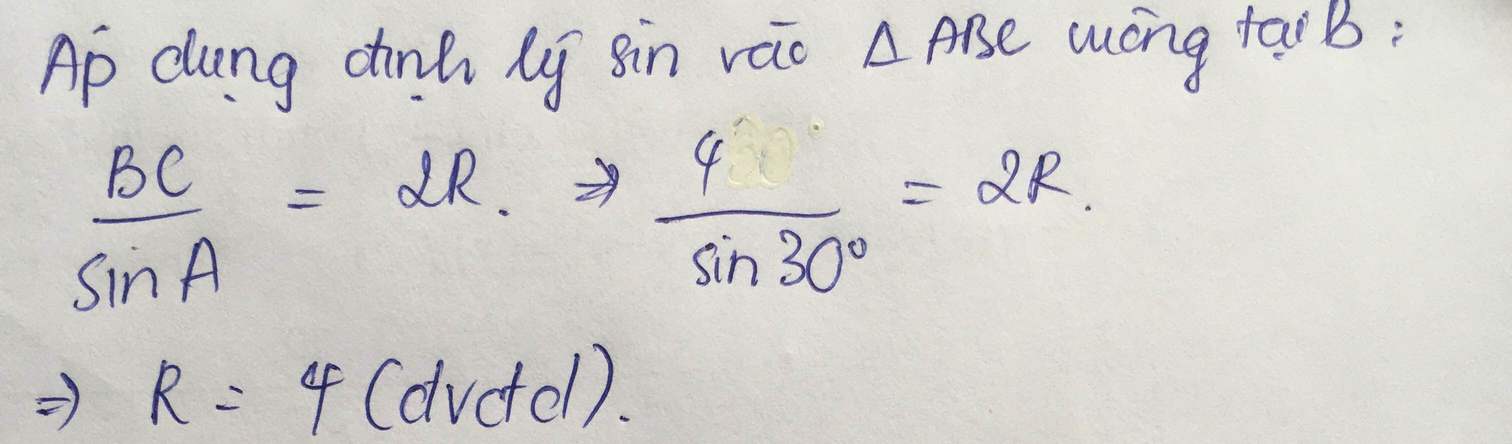Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
PB
Những câu hỏi liên quan
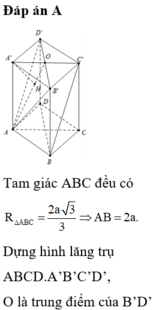
Cho hình lăng trụ tam giác đều ABC.ABC có bán kính đường tròn ngoại tiếp đáy ABC bằng
2
a
3
3
và góc giữa hai đường thẳng AB và BC bằng
60
o
. Tính khoảng cách d giữa hai đường thẳng AB và BC ?
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có bán kính đường tròn ngoại tiếp đáy ABC bằng 2 a 3 3 và góc giữa hai đường thẳng AB' và BC' bằng 60 o . Tính khoảng cách d giữa hai đường thẳng AB' và BC' ?
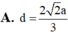
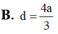
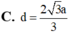
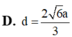
Tam giác ABC có BC = 10 và góc A = 300. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
A. 4
B. 5
C. 8
D. 10
Cho tam giác ABC có \(\widehat{A}=60^0;BC=6\). Tính bán kính đường tròn ngoại tiếp tam giác đó ?
Cho tam giác ABC cân tại A có góc BAC =120 độ và cạnh BC=6.Bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Lời giải:
Ta nhớ lại công thức, trong tam giác $ABC$ có $AB=c, BC=a, CA=b$ thì:
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$.
Ứng vào bài toán, với $\sin A=\sin 120=\frac{\sqrt{3}}{2}$ và $a=BC=6$ thì:
$R=\frac{a}{2\sin A}=\frac{6}{2.\frac{\sqrt{3}}{2}}=2\sqrt{3}$
Đúng 2
Bình luận (0)
Tam giác ABC có AB = 3; AC = 6 và góc A = 600. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
A. 2
B. 3
C. 5
D. 6
Chọn B.
Áp dụng định lí Cosin, ta có
BC2 = AB2 + AC2 - 2AB.AC.cosA
= 32 + 62-2.3.6.cos600 = 27
Ta thấy: BC2 + AB2 = AC2
Suy ra tam giác ABC vuông tại B
do đó bán kính R = AC : 2 = 3.
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc BAC=120 độ, AD là phân giác trong của góc A
CMR: tổng 2 bán kính đường tròn ngoại tiếp tam giác ABD, ADC bằng bán kính đường tròn ngoại tiếp tam giác ABC
Cho tam giác ABC có AB =5a, BC=8a, góc ABC=60 , gọi M là trung điểm của BC. Tính theo a độ dài đoạn AM và bán kính đường tròn ngoại tiếp tam giác ABC.
\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại b và góc bac=30 độ; bc=4 . tính bán kính đường tròn ngoại tiếp tam giác abc
cho tam giác ABC có AB=AC=40, BC=48. gọi O và I thứ tự là tâm đường tròn ngoại tiếp tam và nội tiếp tam giác. tính
a) Bán kính đường tròn nội tiếp
b) Bán kính đường tròn ngoại tiếp
c) Khoảng cách OI