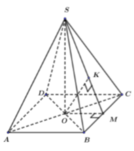
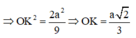Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và khoảng cách từ A đến (SBC) bằng a 6 3 . Thể tích của hình chóp bằng:
A. 6 24 a 3 B. 2 9 a 3
C. 2 8 a 3 D. 2 6 a 3
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng a 3 2 6 . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)
A . a 6 2
B . a 6 3
C . a 6 6
D . a 6
Đáp án B
Gọi M là trung điểm BC; Gọi d là khoảng cách từ A tới (SBC)
Ta có:
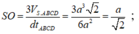
![]()
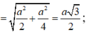
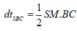
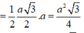
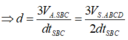
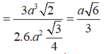
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng a 3 2 6 . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)
A. a 6 3 .
B. a 6 3 .
C. a 6 6 .
D. a 6 .
Đáp án B.
Gọi M là trung điểm BC ; Gọi d là khoảng cách từ A tới (SBC)
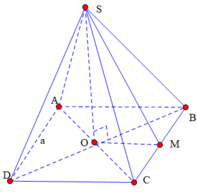
S O = 3 V S . A B C D d t A B C D = 3 a 3 2 6 a 2 = a 2
S M = S O 2 + M O 2 = a 2 2 + a 2 4 = a 3 2
d t S B C = 1 2 S M . B C = 1 2 a 3 2 . a = a 2 3 4
⇒ d = 3 V A . S B C d t S B C = 3 V S . A B C D 2 d t S B C = 3 a 3 2 2.6. a 2 3 4 = a 6 3
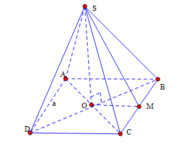
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, SA = SB = SC = SD = a sqrt(3). Tính khoảng cách từ tâm O của hình vuông ABCD đến mặt bên (SBC)
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Khoảng cách từ AD tới (SBC) bằng:
A. a 2 3
B. a 2 3
C. a 3 2
D. không phải các kết quả A, B, C
Gọi O là tâm của hình vuông ABCD , N là trung điểm của BC.
Ta có: AD// BC nên AD// mp(SBC)
d( AD; (SBC)) = d(A; (SBC)) =2.d(O;(SBC)).
* Trong mp( SON) , kẻ OH vuông góc SN. Khi đó, khoảng cách từ O đến (SBC) là OH
O N = 1 2 A B = a 2
Tam giác SBC là tam giác đều đường cao SN nên S N = a 3 2
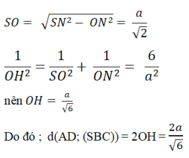
Đáp án A
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 1 cạnh bên hợp với mặt đáy một góc 60 o Khoảng cách từ O đến mặt phẳng (SBC) bằng
A. 1 2
B. 2 2
C. 7 2
D. 42 14
Chọn D.
Lời giải. Xác định
![]()

Gọi M là trung điểm BC, kẻ OK ⊥ SM.
![]()
Tam giác vuông SOM
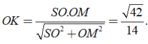
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, cạnh bên hợp với mặt đáy một góc 60 ° . Khoảng cách từ O đến mặt phẳng (SBC) bằng
A. 1 2
B. 2 2
C. 7 2
D. 42 14
Gọi H là trung điểm AD \(\Rightarrow SH\perp\left(ABCD\right)\) và \(SH=\dfrac{a\sqrt{3}}{2}\)
Gọi M là trung điểm BC \(\Rightarrow HM||CD\Rightarrow HM\perp CB\) đồng thời \(HM=CD=a\)
\(\Rightarrow BC\perp\left(SHM\right)\)
Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SBC\right)\)
\(\Rightarrow HK=d\left(H;\left(SBC\right)\right)\)
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{HM^2}\Rightarrow HK=\dfrac{SH.HM}{\sqrt{SH^2+HM^2}}=\dfrac{a\sqrt{21}}{7}\)
\(DH||BC\Rightarrow DH||\left(SBC\right)\Rightarrow d\left(D;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)=\dfrac{a\sqrt{21}}{7}\)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a.
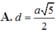
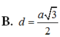
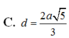

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a.
A. d = a 5 2
B. d = a 3 2
C. d = 2 a 5 3
D. d = a 2 3
Chọn D.
Phương pháp:
Xác định khoảng cách từ O đến 1 mặt bên của hình chóp và sử dụng các hệ thức lượng trong tam giác vuông để làm bài toán.
Cách giải: