Cho hai mặt phẳng:
( P 1 ): 2x + y + 2z + 1 = 0 và ( P 2 ): 4x – 2y – 4z + 7 = 0.
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến ( P 1 ) và ( P 2 ) là bằng nhau.
Trong không gian Oxyz, cho điểm A di động trên mặt phẳng (P): 2x - y - 2z = 0, điểm B di động trên mặt phẳng (Q): 4x - 2y - 4z - 9 = 0. Khoảng cách giữa hai điểm A và B nhỏ nhất là:
A. 3 2
B. 1 4
C. 9 28
D. 9 28
Đáp án A
Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xày ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:
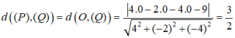
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng 3/2
M cách đều hai mặt phẳng P : 2 x - y + z - 3 = 0 và Q : 4 x - 2 y + 2 z + 1 = 0 là một mặt phẳng (R).
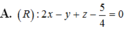
![]()
![]()
![]()
Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 = 0, (Q): 2x - 4y - 4z + m = 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1
A. m=8
B. m=38
C. m=8 hoặc m=-4
D. m=38 hoặc m=-34
Đáp án C
Lấy A(-1; 0; 0) ∈ (P). Ta có
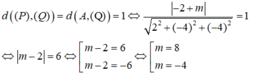
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng có phương trình P : x − y + 4 z − 2 = 0 và Q : 2 x − 2 z + 7 = 0 . Góc giữa hai mặt phẳng (P) và (Q) là
A. 90 0
B. 45 0
C. 60 0
D. 30 0
Đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n P → = 1 ; − 1 ; 4 . Mặt phẳng (Q) có vectơ pháp tuyến là n Q → = 2 ; 0 ; − 2 .
Cách 1: Tư duy tự luận
Góc giữa hai mặt phẳng (P) và (Q) được tính theo công thức:
cos P , Q ^ = cos n P → , n Q → = n P → . n Q → n P → . n Q → = 1.2 + − 1 .0 + 4. − 2 1 2 + − 1 2 + 4 2 . 2 2 + 0 2 + − 2 2
⇔ cos P , Q ^ = 1 2 . Vậy P , Q ^ = 60 0 .
Cách 2: Sử dụng máy tính cầm tay
Nhập vào máy tính các vectơ: VctA = 1 ; − 2 ; 4 , VctB = 2 ; 0 ; − 2 .

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng có phương trình P : x − y + 4 z − 2 = 0 và Q : 2 x − 2 z + 7 = 0 . Góc giữa hai mặt phẳng (P) và (Q) là
A. 90 °
B. 45 °
C. 60 °
D. 30 °
Mặt phẳng alpha qua hai điểm M(1;-1;-1),N (3;-2;3) và vuông góc Bê ta: 2x-3y-3z+4=0 A. Alpha: 6x+2y+2z-1=0 B. Alpha: 3x-4y-z-8=0 C.Alpha: 3x-2y+4z-1=0 D.Alpha: 3x+2y+4z+1=0
\(\overrightarrow{n_{\left(\beta\right)}}=\left(2;-3;-3\right)\)
\(\overrightarrow{MN}=\left(2;-1;4\right)\)
\(\Rightarrow\left[\overrightarrow{n_{\left(\beta\right)}};\overrightarrow{MN}\right]=\left(-15;-14;4\right)\Rightarrow\left(\alpha\right)\) nhận (15;14;-4) là 1 vtpt
Từ vtpt nói trên có thể thấy cả 4 đáp án đều sai
Trong không gian Oxyz, khoảng cách giữa mặt phẳng α : 2x+4y+4z+1=0 và mặt phẳng β : x+2y+2z+2=0 bằng
A. 3 2
B. 1 3
C. 1 2
D. 1
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 4 x - 2 y + 4 z = 0 và mặt phẳng ( P ) : x + 2 y - 2 z + 1 = 0 . Gọi (Q) là mặt phẳng song song với (P) và tiếp xúc với mặt cầu (S). Phương trình mặt phẳng (Q) là
A. ( Q ) : x + 2 y - 2 z - 17 = 0
B. ( Q ) : x + 2 y - 2 z - 35 = 0
C. ( Q ) : x + 2 y - 2 z + 1 = 0
D. ( Q ) : 2 x + 2 y - 2 z + 19 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 4 x - 2 y + 4 z = 0 và mặt phẳng ( P ) : x + 2 y - 2 z + 1 = 0 . Gọi (Q) là mặt phẳng song song với (P) và tiếp xúc với mặt cầu (S). Phương trình mặt phẳng (Q) là:
![]()
![]()
![]()
![]()