Ta có: M(x, y, z) ∈ (P) ⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
![]()
⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|
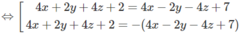
![]()
Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0
Ta có: M(x, y, z) ∈ (P) ⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
![]()
⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|
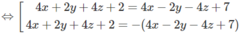
![]()
Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0
Trong không gian Oxyz, cho điểm A di động trên mặt phẳng (P): 2x - y - 2z = 0, điểm B di động trên mặt phẳng (Q): 4x - 2y - 4z - 9 = 0. Khoảng cách giữa hai điểm A và B nhỏ nhất là:
A. 3 2
B. 1 4
C. 9 28
D. 9 28
Trong không gian Oxyz, cho điểm A(1 ;-2 ;3) và mặt phẳng (P) có phương trình x + 2y - 2z + m = 0. Tìm các giá trị của m, biết rằng khoảng cách từ A đến mặt phẳng (P) bằng 1
A. m=12
B. m=18
C. m=18 hoặc m=0
D. m=12 hoặc m=6
Trong không gian Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P) có phương trình x - 2y + 2z + 1 = 0. Khoảng cách từ A đến mặt phẳng (P) là:
A. 8 3
B. - 8 3
C. 8 9
D. 8
Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 = 0, (Q): 2x - 4y - 4z + m = 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1
A. m=8
B. m=38
C. m=8 hoặc m=-4
D. m=38 hoặc m=-34
Cho mặt phẳng P : 2 x + 2 y - 2 z + 15 = 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 y - 2 z - 2 = 0 . Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là:
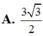
![]()
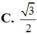
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (α).
Cho hai đường thẳng:
d: x = 6 y = - 2 t z = 7 + t và d 1 : x = - 2 + t ' y = - 2 z = - 11 - t '
Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d 1 đến (P) là bằng nhau.
Trong không gian Oxyz, khoảng cách giữa mặt phẳng α : 2x+4y+4z+1=0 và mặt phẳng β : x+2y+2z+2=0 bằng
A. 3 2
B. 1 3
C. 1 2
D. 1
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng
( P 1 ): 2x + y + 2z + 1 = 0 và ( P 2 ): 2x + y + 2z + 5 = 0.