Trên hình 100 ta có OA = OB, góc OAC = góc OBD. Chứng minh rằng AC = BD
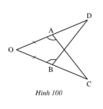
Trên hình 100 ta có \(OA=OB;\widehat{OAC}=\widehat{OBD}\)
Chứng minh rằng AC = BD ?
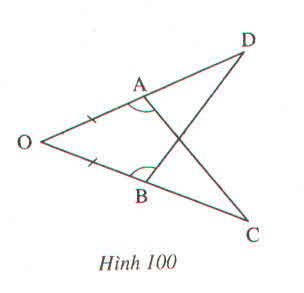
Xét tam giác OAC và tam giác OBD có:
góc OAC= góc OBD (gt)
OA=OB (gt)
góc O là góc chung
Do đó: tam giác OAC = tam giác OBD(g.c.g)
=> AC=BD
Vậy AC=BD
(Cho góc xoy nhỏ hơn 90 độ. Trên tia ox lần lượt lấy điểm A và D(OA<OD). Trên tia oy lần lượt lấy B và C sao cho oa= OB, Góc OAC khác OBD. Chứng minh rằng AC= BD
Những ai hok lớp 7 thj dở lại bài 36 trang 123, sgk toán tập 1
Các bn xem hình và giải nhé(ko cần vẽ hình)
Trên hình 100 ta có OA=OB, OAC=OBD.
a) Chứng minh rằng AC=BD.
b) I là giao điểm của cạnh BD và cạnh AC. Tính tam giác AID và tam giác BIC.
c) Chứng minh OI là tia phân giác của góc COD??
Ai giải đc pái lm sư phụ, mik giải hoài ko ra
bạn lấy đâu ra câu b) và câu c) vậy
Ta có: BC = OC - OB
AD = OD - OA
mà OC = OD ( tam giác OBD = OAC)
OA = OB ( gt)
=> BC = AD
góc IBC + góc IBO = 1800 ( kề bù )
góc OAI + góc OBI = 1800 ( kề bù )
mà góc OAI = góc OBI (tam giác OBD = OAC )
=> góc DAI = góc CBI
Xét tam giác AID và tam giác BIC có :
góc D = góc C ( tam giác OBD = OAC )
AB = CD ( chứng minh trên 0
góc DAI = góc CBI ( cmt )
do đó tam giác AID = tam giác BIC ( g-c-g)
c) Xét tam giác AOI và tam giác BOI có :
OA = OB ( gt )
OI : cạnh chung
AI = BI ( tam giác AID = tam giác BIC )
do đó tam giác OAI = tam giác OBI (c-c-c)
=> góc AOI = góc BOI
Vậy OI là tia phân giác của góc COD
Mình giải rất chi tiết và đầy đủ rồi đó, tick cho mình thiệt nhiều nha mấy bạn !
Những ai hok lớp 7 thj dở lại bài 36 trang 123, sgk toán tập 1
Các bn xem hình và giải nhé(ko cần vẽ hình)
Trên hình 100 ta có OA=OB, OAC=OBD.
a) Chứng minh rằng AC=BD.
b) I là giao điểm của cạnh BD và cạnh AC. Tính tam giác AID và tam giác BIC.
c) Chứng minh OI là tia phân giác của góc COD??
Ai giải đc pái lm sư phụ, mik giải hoài ko ra
Cho góc nhọn xOy . Trên cạnh Ox lấy điểm A và trên cạnh Oy lấy điểm B sao cho OA=OB. Vẽ AC vuông góc với Oy (C thuộc Oy) , BD vuông góc Ox(D thuộc Ox) . Chứng minh:
a)tam giác OBD = tam giác OAC
b)gọi I là giao điểm của AC và BD . chứng minh: IC=ID
c)chứng minh OI là tia phân giác của góc xOy
a, Xét △OBD vuông tại D và △OAC vuông tại C
Có: xOy là cạnh chung
OB = OA (gt)
=> △OBD = △OAC (ch-gn)
b, Vì △OBD = △OAC (cmt) => OD = OC (2 cạnh tương ứng) và OBD = OAC (2 góc tương ứng)
Ta có: OD + AD = OA và OC + CB = OB
Mà OA = OB (gt) ; OD = OC (cmt)
=> AD =BC
Xét △CIB vuông tại C và △DIA vuông tại D
Có: BC = AD (cmt)
CBI = DAI (2 góc tương ứng)
=> △CIB = △DIA (cgv-gnk)
=> IC = ID (2 cạnh tương ứng)
c, Xét △AOI và △BOI
Có: OA = OB (gt)
OI là cạnh chung
IA = IB (△DIA = △CIB)
=> △AOI = △BOI (c.c.c)
=> AOI = BOI (2 góc tương ứng)
=> OI là tia phân giác của góc AOB
hay OI là tia phân giác của góc xOy
Cho góc nhọn xOy . Trên cạnh Ox lấy điểm A và trên cạnh Oy lấy điểm B sao cho OA=OB. Vẽ AC vuông góc với Oy (C thuộc Oy) , BD vuông góc Ox(D thuộc Ox) . Chứng minh:
a)tam giác OBD = tam giác OAC
b)gọi I là giao điểm của AC và BD . chứng minh: IC=ID
c)chứng minh OI là tia phân giác của góc xOy
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên Oy lấy điểm B sao cho OA=OB. Trên tia Ax lấy điểm D, trên tia By lấy điểm C sao cho AD=BC.
a, Chứng minh ΔAOC=ΔBOD và \(\widehat{OAC}\)=\(\widehat{OBD}\)
b, Gọi N lầ giao điểm của AC và BD. Chứng minh ΔADN=ΔBCN và ON là phân giác của \(\widehat{xOy}\)
c, Gọi H,K lần lượt là giao điểm của ON với DC và AB. Chứng minh OH⊥CD, AB//CD.
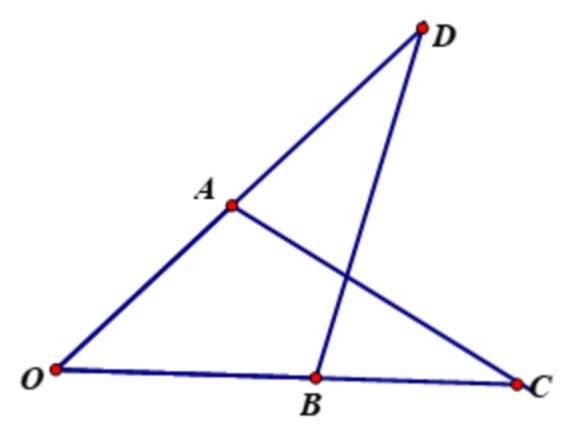
Cho hình vẽ sau, biết OA = OB; góc OAC = góc OBD.
a) Chứng minh rằng AC = BD; OC = OD; AD = BC.
b) Chứng minh rằng tam giác ADC = tam giác BCD.
c) Gọi I là giao điểm của AC và BD. Chứng minh rằng IA = IB và IC = ID.
d) Chứng minh rằng OI là tia phân giác của góc AOB và OI vuông góc CD.
a: Xét ΔOBD và ΔOAC có
\(\widehat{OBD}=\widehat{OAC}\)
OB=OA
\(\widehat{BOD}\) chung
Do đó: ΔOBD=ΔOAC
=>BD=AC; OD=OC
OB+BC=OC
OA+AD=OD
mà OB=OA và OC=OD
nên BC=AD
b: Xét ΔADC và ΔBCD có
AD=BC
CD chung
AC=BD
Do đó: ΔADC=ΔBCD
c: ΔADC=ΔBCD
=>\(\widehat{IDC}=\widehat{ICD}\)
=>ΔIDC cân tại I
=>ID=IC
ID+IB=BD
IC+IA=AC
mà ID=IC và BD=AC
nên IB=IA
d: Xét ΔOAI và ΔOBI có
OA=OB
AI=BI
OI chung
Do đó: ΔOAI=ΔOBI
=>\(\widehat{AOI}=\widehat{BOI}\)
=>OI là phân giác của góc AOB
=>OI là phân giác của góc COD
ΔCOD cân tại O
mà OI là đường phân giác
nên OI\(\perp\)CD
a, xét tam giác OBD và tam giác OAC có:
góc O chung
OA=OB(gt)
góc OAC= góc OBD(gt)
=>tam giác OBD= tam giác OAC (g.c.g)
=>\(\left\{{}\begin{matrix}AC=BD\\OC=OD\end{matrix}\right.\)(2 cạnh tương ứng)
b, Nối D với C
Xét tam giác ADC và tam giác BCD có:
AD=BC ( cmt)
BD=AC(cmt)
CD cạnh chung
=>tam giác ADC =tam giác BCD (c.c.c)
Cho góc nhọn xOy. Trên cạnh Ox lấy điểm A và trên cạnh Oy lấy điểm B sao cho OA = OB. Vẽ AC vuông góc với Oy (C thuộc Oy),BD vuông góc với Ox.Chứng minh tam giác OBD bằng tam giác OAC