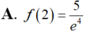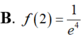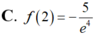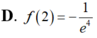Cho hàm số y = f(x) = x2.
Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).
Cho hàm số y = f ( x ) = x 2 .
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).
c) Dùng đồ thị để ước lượng các giá trị ( 0 , 5 ) 2 ; ( - 1 , 5 ) 2 ; ( 2 , 5 ) 2 .
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số √3 ; √7.
a) Ta có bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 4 |
Vẽ đồ thị hàm số :
Trên hệ trục tọa độ xác định các điểm (-2 ; 4) ; (-1 ; 1) ; (0 ; 0) ; (1 ; 1) ; (2 ; 4). Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = x 2 .
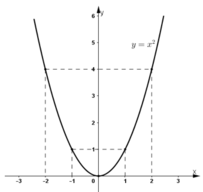
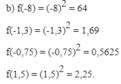
c)
– Để ước lượng giá trị ( 0 , 5 ) 2 ta tìm điểm A thuộc đồ thị có hoành độ là 0,5. Khi đó, tung độ của điểm A chính là giá trị ( 0 , 5 ) 2 . Từ điểm (0,5;0) trên trục hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm A. Từ điểm A trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của ( 0 , 5 ) 2
– Để ước lượng giá trị ( - 1 , 5 ) 2 ta tìm điểm B thuộc đồ thị có hoành độ là -1,5. Khi đó, tung độ của điểm B chính là giá trị ( - 1 , 5 ) 2 . Từ điểm (-1,5;0) trên trục hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm B. Từ điểm B trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của ( - 1 , 5 ) 2
– Để ước lượng giá trị ( 2 , 5 ) 2 ta tìm điểm C thuộc đồ thị có hoành độ là 2,5. Khi đó, tung độ của điểm C chính là giá trị ( 2 , 5 ) 2 . Từ điểm (2,5;0) trên trục hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm C. Từ điểm C trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của ( 2 , 5 ) 2
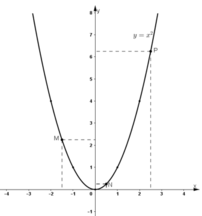
Trên đồ thị hàm số, lấy các điểm M, N, P có hoành độ lần lượt bằng -1,5 ; 0,5 và 2,5.
Dựa vào đồ thị nhận thấy các điểm M, N, P có tọa độ là : M(-1,5 ; 2,25) ; N(0,5 ; 0,25) ; P(2,5 ; 6,25).
Vậy ( 0 , 5 ) 2 = 2 , 25 ; ( - 1 , 5 ) 2 = 2 , 25 ; ( 2 , 5 ) 2 = 6 , 25 .
d)
– Để ước lượng vị trí điểm biểu diễn số √3 trên trục hoành ta tìm điểm M thuộc đồ thị có tung độ là ( √ 3 ) 2 = 3 . Khi đó, hoành độ của điểm M chính là vị trí điểm biểu diễn √3. Từ điểm (0;3) trên trục tung ta kẻ đường thẳng song song với Ox cắt đồ thị tại điểm M. Từ điểm M trên đồ thị kẻ đường thẳng song song với Oy ta xác định được hoành độ của điểm M chính là vị trí điểm biểu diễn √3
– Để ước lượng vị trí điểm biểu diễn số √7 trên trục hoành ta tìm điểm N thuộc đồ thị có tung độ là ( √ 7 ) 2 = 7 . Khi đó, hoành độ của điểm N chính là vị trí điểm biểu diễn √7. Từ điểm (0;7) trên trục tung ta kẻ đường thẳng song song với Ox cắt đồ thị tại điểm N. Từ điểm N trên đồ thị kẻ đường thẳng song song với Oy ta xác định được hoành độ của điểm N chính là vị trí điểm biểu diễn √7
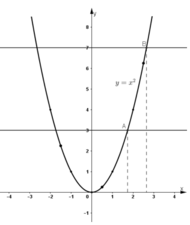
Ta có : ( √ 3 ) 2 = 3 ; ( √ 7 ) 2 = 7
⇒ Các điểm (√3 ; 3) và (√7 ; 7) thuộc đồ thị hàm số y = x 2
Để xác định các điểm √3 ; √7 trên trục hoành, ta lấy trên đồ thị hàm số các điểm A, B có tung độ lần lượt là 3 và 7.
Chiếu vuông góc các điểm A, B trên trục hoành ta được các điểm √3 ; √7 trên đồ thị hàm số.
Cho hàm số y = f(x) = -2 x 2 . Tổng các giá trị a của thỏa mãn f(a) = - 8 + 4 3 là:
A. 1
B. 0
C. 10
D. -10
Cho hàm số y = f(x) = x2.
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).
c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2.
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số √3; √7.
Cho hàm số y=f(x)=2x-3. X lấy giá trị thực bất kì x1, x2 sao cho x1 < x2. Chứng tỏ f(x1) < f(x2). Kết luận về tính biến thiên của hàm số
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Cho hàm số y = f(x) = -1,5 x 2
Hãy tính f(1), f(2), f(3) rồi sắp xếp các giá trị này theo thứ tự từ lớn đến bé.
Ta có: f(1) = -1,5. 1 2 = -1,5
f(2) = -1,5. 2 2 = -6
f(3) = -1,5. 3 2 = -13,5
Theo thứ tự từ lớn đến bé : -1,5; -6; -13,5.
Cho hàm số y = f(x) = -1,5 x 2
Hãy tính f(-3), f(-2), f(-1) rồi sắp xếp các giá trị này theo thứ tự từ bé đến lớn.
Ta có: f(-3)= -1,5. - 3 2 = -13,5
f(-2) = -1,5. - 2 2 = -6
f(-1) = -1,5. - 1 2 = -1,5
Theo thứ tự từ bé đến lớn : -13,5 ; -6 ; -1,5.
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 , ∀ x ∈ R và f(1)=0 Tính giá trị f(2).