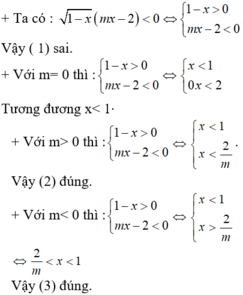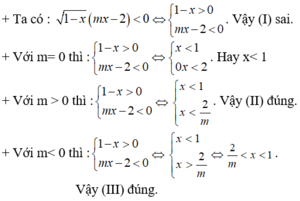Cho phương trình x 2 − 2 m + 1 x + m − 1 = 0 (m là tham số). Tìm m để phương trình có hai nghiệm phân biệt x 1 , x 2 thỏa mãn 3 x 1 + x 2 = 0 .
PB
Những câu hỏi liên quan
Cho bất phương trình :
1
-
x
(
m
x
-
2
)
0
(
*
)
Xét các mệnh đề sau: (1) Bất phương trình tương đương với mx - 2 0 (2) m ≥ 0 là điều kiện cần để mọi x 1 là nghiệm của bất phương trình (*) (3) Với m 0 , tập nghiệm của bất phương trình là 2/m x 1 Mệnh...
Đọc tiếp
Cho bất phương trình : 1 - x ( m x - 2 ) < 0 ( * ) Xét các mệnh đề sau:
(1) Bất phương trình tương đương với mx - 2 <0
(2) m ≥ 0 là điều kiện cần để mọi x< 1 là nghiệm của bất phương trình (*)
(3) Với m < 0 , tập nghiệm của bất phương trình là 2/m< x< 1
Mệnh đề nào đúng?
A. Chỉ (1)
B. Chỉ (3)
C. (2) và (3)
D. Tất cả đúng
Cho bất phương trình :
1
-
x
(
mx
-
2
)
0
(
*
)
Xét các mệnh đề sau: (I) Bất phương trình tương đương với mx - 2 0; (II) m ≥ 0 là điều kiện cần để mọi x 1 là nghiệm của bất phương trình (*) (III) Với m 0 , tập nghiệm của bất phương trình là
2...
Đọc tiếp
Cho bất phương trình : 1 - x ( mx - 2 ) < 0 ( * )
Xét các mệnh đề sau:
(I) Bất phương trình tương đương với mx - 2 < 0;
(II) m ≥ 0 là điều kiện cần để mọi x < 1 là nghiệm của bất phương trình (*)
(III) Với m < 0 , tập nghiệm của bất phương trình là 2 m < x < 1
Mệnh đề nào đúng?
A. Chỉ (I)
B. Chỉ (III)
C. (II) và (III)
D. Cả (I), (II), (III)
Bài 1. Tìm giá trị của K sao cho
a, Phương trình: 2x + k x-1 có nghiệm x-2
b, Phương trình: (2x+1) (9x+2k) - 5(x+2)40 có nghiệm x2
c, Phương trình: 2(2x+1)+18+3(x+2) (2x+k) có nghiệm x1
d, Phương trình: 5(m+3x) (x+1)- 4(1+2x) 80 có nghiệm x2
Bài 2. Tìm các giá trị của m, a và b để các cặp phương trình sau đây tương đương:
a, mx2-(m+1) x+1 0 và (x-1) (2x-1) 0
b,(x-3) (ax+2) 0 va...
Đọc tiếp
Bài 1. Tìm giá trị của K sao cho
a, Phương trình: 2x + k= x-1 có nghiệm x=-2
b, Phương trình: (2x+1) (9x+2k) - 5(x+2)=40 có nghiệm x=2
c, Phương trình: 2(2x+1)+18+=3(x+2) (2x+k) có nghiệm x=1
d, Phương trình: 5(m+3x) (x+1)- 4(1+2x) =80 có nghiệm x=2
Bài 2. Tìm các giá trị của m, a và b để các cặp phương trình sau đây tương đương:
a, mx2-(m+1) x+1= 0 và (x-1) (2x-1)= 0
b,(x-3) (ax+2)= 0 và (2x+b) (x+1)= 0
Bài 1. Tìm giá trị của K sao cho
a, Phương trình: 2x + k x-1 có nghiệm x-2
b, Phương trình: (2x+1) (9x+2k) - 5(x+2)40 có nghiệm x2
c, Phương trình: 2(2x+1)+18+3(x+2) (2x+k) có nghiệm x1
d, Phương trình: 5(m+3x) (x+1)- 4(1+2x) 80 có nghiệm x2
Bài 2. Tìm các giá trị của m, a và b để các cặp phương trình sau đây tương đương:
a, mx2-(m+1) x+1 0 và (x-1) (2x-1) 0
b,(x-3) (ax+2) 0 và (2x+b) (x+1) 0
Đọc tiếp
Bài 1. Tìm giá trị của K sao cho
a, Phương trình: 2x + k= x-1 có nghiệm x=-2
b, Phương trình: (2x+1) (9x+2k) - 5(x+2)=40 có nghiệm x=2
c, Phương trình: 2(2x+1)+18+=3(x+2) (2x+k) có nghiệm x=1
d, Phương trình: 5(m+3x) (x+1)- 4(1+2x) =80 có nghiệm x=2
Bài 2. Tìm các giá trị của m, a và b để các cặp phương trình sau đây tương đương:
a, mx2-(m+1) x+1= 0 và (x-1) (2x-1)= 0
b,(x-3) (ax+2)= 0 và (2x+b) (x+1)= 0
https://i.imgur.com/0Ega507.jpg
Cho phương trình ẩn x: (m^2-m+1)x + 2m - 3 = 0.
Tìm m để phương trình không là phương trình bậc nhất một ẩn
Để pt không là phương trình bậc nhất 1 ẩn thì m^2 - m + 1 = 0
<=> m^2 - m + 1/4 + 3/4 = 0
<=> (m - 1/2)^2 + 3/4 = 0 (1)
Mà (m - 1/2)^2 >= 0 nên (m - 1/2)^2 + 3/4 >= 3/4 > 0. Mâu thuẫn với (1) => Không có giá trị m nào thỏa mãn.
P/s: Mìnk cx chẳng chắc nhưng theo mình thì không có m nào thỏa mãn đề bài yêu cầu.
Đúng 0
Bình luận (0)
Cho bất phương trình:
m
x
2
+
2
(
m
-
1
)
x
+
m
+
2
0
. Điều kiện của tham số m để bất phương trình đã cho vô nghiệm là A. m 0 B.
m
≤
0
C.
m
≥
1
4
D.
m
≤
1
4
Đọc tiếp
Cho bất phương trình: m x 2 + 2 ( m - 1 ) x + m + 2 < 0 . Điều kiện của tham số m để bất phương trình đã cho vô nghiệm là
A. m > 0
B. m ≤ 0
C. m ≥ 1 4
D. m ≤ 1 4
+ Khi m = 0, bất phương trình trở thành - 2 x + 2 < 0 ⇔ x > 1 . Vậy m = 0 không thỏa mãn yêu cầu của bài toán.
+ Khi m ≠ 0 , bất phương trình vô nghiệm khi m x 2 + 2 m - 1 x + m + 2 ≥ 0 , ∀ x ∈ ℝ . ⇔ a > 0 ∆ ' ≤ 0 ⇔ m > 0 ( m - 1 ) 2 - m ( m + 2 ) ≤ 0 .
⇔ m > 0 - 4 m + 1 ≤ 0 ⇔ m > 0 m ≥ 1 4 ⇔ m ≥ 1 4
Chọn C.
Đúng 0
Bình luận (0)
Bài 1: Cho phương trình bậc hai 2x2 -(m+3)x+ m=0. Gọi x1 và x2 là 2 nghiệm của pt. Tình gt nhỏ nhất của biểu thức
P= | x1- x2|
Bài 2: Cho phương trình bậc hai x2 - 2mx+2m-1=0. Với gt nào của m thì phương trình có 2 nghiệm thoả mãn x1=3x2
cho phương trình x2 - 2x - 2m2 = 0
a) Giải phương trình khi m = 0
b) Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: x12 = 4x22
Cho bất phương trình \(\left(m+1\right)x^2-2\left(m+2\right)x+4>0\) . Tìm m để với mọi x thuộc [ 0 , 1] đều là nghiệm của bất phương trình
CHo phương trình : x2 - ( 2m + 2 )x + m2 + 2m + 0
a) Tìm m để phương trình trên nhận 4 + căn 2019 làm nghiệm
b) Tìm m để phương trình có hai nghiệm x1 x2 thoả mãn x1 -x2 = m2 +2
a, Vì pt trên nhận \(4+\sqrt{2019}\) là nghiệm nên
\(\left(4+\sqrt{2019}\right)^2-\left(2m+2\right)\left(4+\sqrt{2019}\right)+m^2+2m=0\)
\(\Leftrightarrow2035+8\sqrt{2019}-2m\left(4+\sqrt{2019}\right)-8-2\sqrt{2019}+m^2+2m=0\)
\(\Leftrightarrow m^2-2m\left(3+\sqrt{2019}\right)+6\sqrt{2019}+2027=0\)
Có \(\Delta'=\left(3+\sqrt{2019}\right)^2-6\sqrt{2019}-2027=1>0\)
Nên pt có 2 nghiệm \(m=\frac{3+\sqrt{2019}-1}{1}=2+\sqrt{2019}\)
hoặc \(m=\frac{3+\sqrt{2019}+1}{1}=4+\sqrt{2019}\)
b, Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=2m+2\left(1\right)\\x_1x_2=m^2+2m\left(2\right)\end{cases}}\)
Theo đề \(x_1-x_2=m^2+2\left(3\right)\)
Lấy (1) + (3) theo từng vế được
\(2x_1=m^2+2m+5\)
\(\Rightarrow x_1=\frac{m^2+2m+5}{2}\)
\(\Rightarrow x_2=2m+2-x_1=...=-\frac{\left(m-1\right)^2}{2}\)
Thay vào (2) được \(\frac{m^2+2m+5}{2}.\frac{-\left(m-1\right)^2}{2}=m^2+2m\)
\(\Leftrightarrow-\left(m^2+2m+5\right)\left(m-1\right)^2=4m^2+8m\)
hmmm
Đúng 0
Bình luận (0)