Cho hai đường thẳng (d): y = − x + m + 2 và (d’): y = ( m 2 − 2 ) x + 3 . Tìm m để (d) và (d’) song song với nhau
PB
Những câu hỏi liên quan
Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho t...
Đọc tiếp
Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho tam giác OPQ vuông tại Q.
cho hai dường thẳng d :y=(m^2-3m+5)x+m-1 và đường thẳng d':y=(m=2)x+5-m,tìm m để hai đương thẳng song song với nhau
Để 2 đường thẳng d và d' song song với nhau thì
\(\left\{{}\begin{matrix}m^2-3m+5=m+2\\m-1\ne5-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+3=0\\2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(m-3\right)=0\\m\ne3\end{matrix}\right.\)
\(\Leftrightarrow m=1\left(tm\right)\)
Đúng 0
Bình luận (0)
Trên mặt phẳng toại độ Oxy, cho đường thẳng (d):y=(m-1)x-m với m là tham số.
Tìm m để (d) đồng quy với hai đường thẳng (d'):y=x - `2/3` và (d''):y=-x+1
Tọa độ giao điểm của (d') với (d'') là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x-\dfrac{2}{3}=-x+1\\y=-x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+x=\dfrac{2}{3}+1\\y=-x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{5}{3}\\y=-x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}\\y=-\dfrac{5}{6}+1=\dfrac{1}{6}\end{matrix}\right.\)
Thay x=5/6 và y=1/6 vào (d), ta được:
\(\dfrac{5}{6}\left(m-1\right)-m=\dfrac{1}{6}\)
=>\(\dfrac{5}{6}m-\dfrac{5}{6}-m=\dfrac{1}{6}\)
=>\(-\dfrac{1}{6}m=1\)
=>m=-1:1/6=-6
Đúng 2
Bình luận (0)
Cho hai đường thẳng d: y = x + 2m, d′: y = 3x + 2 (m là tham số). Tìm m để ba đường thẳng d, d′ và d′′: y = −mx + 2 phân biệt đồng quy.
A. m = −1
B. m = 3
C. m = 1
D. m = −3
Bài 3
Cho hàm số bậc nhất y = (m – 2)x + 2 – m với m là tham số, có đồ thị là đường thẳng d.
1) Vẽ đường thẳng d trên mặt phẳng tọa độ Oxy với m = 3
2) Cho hai đường thẳng d1: y = x + 2 và d2: y = 4 – 3x. Tìm m để ba đường thẳng d, d1, d2 đồng quy.
2: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=4-3x\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=1/2 và y=5/2 vào (d), ta được:
\(\dfrac{1}{2}m-1+2-m=\dfrac{5}{2}\)
=>-1/2m=3/2
hay m=-3
Đúng 1
Bình luận (0)
Cho hai đường thẳng d: y= x+ 2m và d’: y= 3x+2 ( m là tham số). Có mấy giá trị của m để ba đường thẳng d; d’ và d’’: y= -mx+ 2 phân biệt đồng quy.
A.0
B. 1
C. 2
D. 3
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
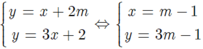
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
Đúng 0
Bình luận (0)
Cho hai đường thẳng (d) : y = -x + m + 2 và (d') : y = (m2 - 2)x + 3.
Tìm m để (d) và (d') song song với nhau.
Cho hai đường thẳng: (D): 2m(m + 1)x - y = -m - 1 và (D'): 4(m - 2)x + y = 3m - 1. Xác định m để D // D'.
Cho hai đường thẳng d và d'. Tìm m để hai đường thẳng: cắt nhau, song song, đồng quy
a) d: 2mx+(m-1).y-2=0, d': (m+2).x+(2m+1).y-(m+2)=0
b) d: (m-2).x+(m-6).y+m-1=0, d': (m-4).x+(2m-3).y+m-5=0




