Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
Hàm số nghịch biến
Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
a) Hàm số đồng biến;
b) Hàm số nghịch biến.
a) Hàm số đồng biến là y = 2x + 5
b) Hàm số nghịch biến là y = -0,5x + 3
Các bài giải bài tập Toán 9 Tập 1 khác:
Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
Hàm số đồng biến
Cho 2 ví dụ về hàm số bậc nhất, trong đó 1 hàm số đồng biến, 1 hàm số nghịch biến
Hàm số đồng biến: y=x+10
Hàm số nghịch biến: y=-x+6
Nêu các bước vẽ đồ thị hàm số y = ax (a khác 0) (đã học ở lớp 7)
cho ví dụ về hàm số bậc nhất trong các trường hợp đồng biến , nghịch biến ![]()
![]() giúp với
giúp với
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.
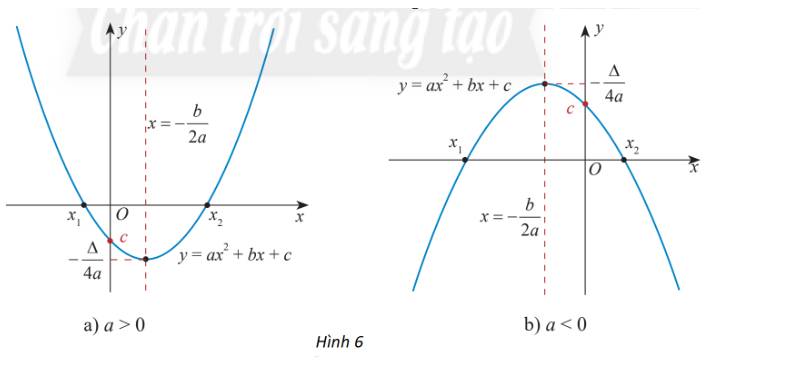
a)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các các hệ số a, b của chúng và xét xem hàm số bậc nhất này đồng biến hay nghịch biến?
y = -0,5x
y = -0,5x là hàm số bậc nhất có a = -0,5, b = 0, nghịch biến vì a = -0,5 < 0
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các các hệ số a, b của chúng và xét xem hàm số bậc nhất này đồng biến hay nghịch biến?
y = 2x2 + 3
y = 2x2 + 3 không phải là hàm số bậc nhất (vì số mũ của x là 2)
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các các hệ số a, b của chúng và xét xem hàm số bậc nhất này đồng biến hay nghịch biến?
y = 1 – 5x
y = 1 – 5x là hàm số bậc nhất có a = -5, b = 1, nghịch biến vì a = -5 < 0
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các các hệ số a, b của chúng và xét xem hàm số bậc nhất này đồng biến hay nghịch biến?
y = √2(x - 1) + √3
y = √2(x - 1) + √3 = √2 x + √3 - √2 là hàm số bậc nhất có a = √2, b = √3 - √2, đồng biến vì a = √2 > 0