Cho hình 36. Hãy viết hệ thức giữa:
Các cạnh góc vuông p, r và đường cao h.
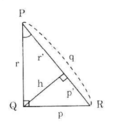
Hình 36
PB
Những câu hỏi liên quan
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông p, r và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
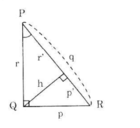
Hình 36
a) p 2 = p ' . q ; r 2 = r ' . q
c) h 2 = p ' . r '
Đúng 0
Bình luận (0)
Cho hình 36. Hãy viết hệ thức giữa:
Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
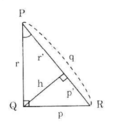
Hình 36
Cho hình 36.
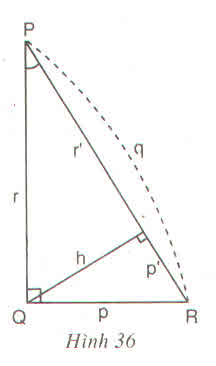
Hãy viết hệ thức giữa :
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền
b) Các cạnh góc vuong p, r và đường cao h
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
Cho hình 36. Hãy viết hệ thức giữa:
Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
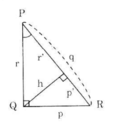
Hình 36
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH.
a) Hãy viết hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền
b) Tính AH biết BH = 4cm; HC = 9cm
\(a,AH^2=BH.BC\)
\(b,\)Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\),đường cao \(AH\) có:
\(AH^2=BH.BC\)
\(\Rightarrow AH^2=4.9\)
\(\Rightarrow AH^2=36\Rightarrow AH=6\left(cm\right)\)
Đúng 1
Bình luận (1)
Cho tam giác vuông tại A đường cao AH
A. Hãy viết hệthức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền
B. Tính AH biết BH:4cm HC:9cm
Cho tam giác ABC vuông tai A đường cao AH
A. Hãy viết hệ thức liên hệ giữa đường cao va hình chiếu của các cạch góc vuông trên canh huyền
B. Tinh AH biết BH=4cm HC=9cm
A. Hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền: \(AH^2=BH.CH\)
B. Ta có △ABC vuông tại A có đường cao AH\(\Rightarrow AH^2=BH.CH=4.9=36\Rightarrow AH=6\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác IRS vuông tại I. Có IH là đường cao.
Câu 1: Viết 5 hệ thức về cạnh và đường cao trong tam giác vuông.
Câu 2: Biết hình chiếu của 2 cạnh góc vuông lần lượt là 9cm và 16cm.Tính các cạnh còn lại trong tam giác vuông đó.
Cho hình trụ bán kính r và có chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sin của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy ?
Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25
Đúng 1
Bình luận (0)