Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài:
OH và OK, nếu biết AB > CD.
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài:
a) OH và OK, nếu biết AB > CD.
b) AB và CD, nếu biết OH < OK.
a) Nếu AB > CD thì HB > KD
⇒ HB2 > KD2
Mà : OH2 + HB2 = OK2 + KD2
⇒ OH2 < OK2
⇒ OH < OK
b) Nếu OH < OK thì OH2 < OK2
⇒ HB2 > KD2 ⇒ HB > KD
⇒ AB > CD
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài: AB và CD, nếu biết OH < OK.
Nếu OH < OK thì OH2 < OK2
⇒ HB2 > KD2 ⇒ HB > KD
⇒ AB > CD
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
a) Nếu AB = CD thì OH = OK.
b) Nếu OH = OK thì AB = CD.
OH là một phần đường kính vuông góc với dây AB
⇒ H là trung điểm của AB ⇒ AB = 2HB
OK là một phần đường kính vuông góc với dây CD
⇒ K là trung điểm của CD ⇒ CD = 2KD
Theo mục 1: OH2 + HB2= OK2+ KD2
a) Ta có: AB = CD ⇒ HB = KD
⇒ OH2 = OK2 ⇒ OH = OK
b) Ta có: OH = OK ⇒ HB2 = KD2
⇒ HB = KD ⇒ AB = CD
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Nếu AB = CD thì OH = OK.
OH là một phần đường kính vuông góc với dây AB
⇒ H là trung điểm của AB ⇒ AB = 2HB
OK là một phần đường kính vuông góc với dây CD
⇒ K là trung điểm của CD ⇒ CD = 2KD
Theo mục 1: OH2 + HB2= OK2+ KD2
Ta có: AB = CD ⇒ HB = KD
⇒ OH2 = OK2 ⇒ OH = OK
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Nếu OH = OK thì AB = CD.
Ta có: OH = OK ⇒ HB2 = KD2
⇒ HB = KD ⇒ AB = CD
Hãy sừ dụng kết quq của bài toán mục 1 để so sánh các độ dài :
a. OH và OK nếu biết AB > CD
b. AB và CD nếu biết OH<OK
Bài 15 (trang 106 SGK Toán 9 Tập 1)
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
a) OH và OK
b) ME và MF
c) MH và MK.
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
ME2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> (Định lý 2 - trang 103).
MF2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> (Định lý 2 - trang 103).
ME2>MF2⇔MH>MK" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
a) Trong đường tròn nhỏ: .
b) Trong đường tròn lớn : .
c) Trong đường tròn lớn : .
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
OH và OK
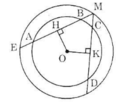
Hình 70
Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
Cho đường tròn (O;5). Vẽ 2 dây AB = 6cm và CD = 8cm. So sánh khoảng cách từ tâm O đến 2 dây AB và CD. HD: Kẻ OH^AB (OH là khoảng cách từ O đến AB); OK^CD (OK là khoảng cách từ O đến CD) Sử dụng định lí 2 bài 2 và định lí Py – ta – go để tính OH và OK.