Cứ hai đỉnh của đa giác    đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).

Khi đó số đường chéo là: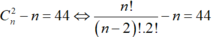 

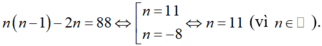
Chọn A.

Chọn B

Ta có: n ( n − 3 ) 2 = 44

ó n² – 3n – 88 = 0

ó (n – 11) (n + 8) = 0

⇔ n − 11 = 0 n + 8 = 0

⇔ n = 12 ( t m ) n = − 9 ( k t m )

Số cạnh của đa giác là 11

Đáp án cần chọn là: A

a) Số đường chéo của đa giác đó :

 \(\frac{\left(8-3\right).8}{2}=20\)( đường chéo )

b) Tổng số đo các góc của đa giác là :

\(108.\left(8-2\right)=108.6=1080\)độ

c) Số đo mỗi góc của đa giác đều 8 cạnh :

\(1080:8=135\)độ

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )

Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n  ⇔ n 2 - 3 n - 2 n = 0

⇔ n 2 - 5 n = 0 ⇔ n ( n - 5 ) = 0  ⇔ 

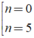
So sánh điều kiện ta có n = 5 thỏa mãn.

Chọn A

Cứ  đỉnh của đa giác sẽ tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).

Khi đó có  cạnh.

Số đường chéo là 66-12=54.

Chọn D.

số đường chéo của đa giác là : \(\frac{n\left(n-3\right)}{2}=\frac{9\left(9-3\right)}{2}=27\)

k mình nha !