Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang là:
A. 6 10
B. 6!
C. A 10 6
D. C 10 6
Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang là:
A. 6 10
B. 6 !
C. A 10 6
D. C 10 6
Đáp án C
Phương pháp:
Sử dụng các quy tắc đếm cơ bản.
Cách giải:
Vì có 10 ghế nên bạn thứ nhất có 10 cách xếp.
Bạn thứ hai có 9 cách xếp.
Bạn thứ ba có 8 cách xếp.
Bạn thứ tư có 7 cách xếp.
Bạn thứ năm có 6 cách xếp.
Bạn thứ sáu có 5 cách xếp.
Như vậy có: 10.9.8.7.6.5 = A 10 6 cách xếp
Một nhóm 10 học sinh gồm 6 nam và 4 nữ. Trong 6 bạn nam có An, trong 4 bạn nữ có Bình. Xếp 10 bạn trên ngồi vào 10 ghế trên một hàng ngang (10 ghế được đánh số từ 1 đến 10 từ trái qua phải). Có bao nhiêu cách sắp xếp thỏa mãn giữa 2 bạn nữ gần nhau có 2 bạn nam đồng thời An không ngồi cạnh Bình
Có 6 học sinh và 3thầy giáo A, B, C ngồi trên một hàng ngang có 9 ghế. Số cách xếp chỗ ngồi cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là
A. 43200
B. 94536
C. 55012
D. 35684
Chọn A
Xếp 6 học sinh có 6! cách xếp.
Giữa 6 học sinh có 5 khoảng trống.
Xếp 3 thầy giáo A, B, C vào 5 khoảng trống trên có: A 5 3 cách.
Vậy số cách xếp thỏa mãn yêu cầu là: 6!. A 5 3 = 43200 cách.
Có bao nhiêu cách xếp chỗ cho 4 bạn nữ và 6 bạn nam ngồi vào 10 ghế mà không có hai bạn nữ nào ngồi cạnh nhau, nếu
a) Ghế sắp thành hàng ngang?
b) Ghế sắp quanh một bàn tròn?
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có 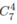 cách.
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có 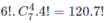 cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có 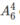 cách.
cách.
Theo quy tắc nhân, có 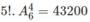 cách.
cách.
Một bàn dài có 2 dãy ghế đối diện với nhau, mỗi dãy gồm 6 ghế. Người ta muốn sắp xếp chỗ ngồi cho 6 học sinh trường A và 6 học sinh trường B vào bàn nói trên. Hỏi có bao nhiêu cách xếp chỗ ngồi trong mỗi trường hợp sau:
a) Bất kì 2 học sinh nào ngồi cạnh nhau hoặc đối diện trường khác nhau.
b) Bất kì 2 học sinh nào ngồi đối diện nhau thì khác trường nhau
a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.
Có bao nhiêu cách xếp chỗ cho 4 bạn nữ và 6 bạn nam ngồi vào 10 ghế mà không có hai bạn nữ nào ngồi cạnh nhau, nếu :
a) Ghế sắp thành hàng ngang ?
b) Ghế sắp quanh một bàn tròn
Số cách sắp xếp 4 người ngồi vào 4 trong 10 chiếc ghế trên một hàng ngang là?
A. 4 !
B. C 10 4 .
C. 4 10
D. A 10 4 .
Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C ngồi vào hàng ghế đó sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp C không ngồi cạnh học sinh lớp B bằng:
A. 1/5
B. 4/5
C. 2/15
D. 2/5
Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C ngồi vào hàng ghế đó sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp C không ngồi cạnh học sinh lớp B bằng?
A. 1/5
B. 4/5
C. 2/15
D. 2/5
`n(\Omega)=6! =720`
`@TH1:` H/s lớp `C` ngồi đầu tiên hoặc cuối cùng.
`=>` Có `2.1.A_3 ^1 .4! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
`@TH2:` H/s lớp `C` không ngồi đầu cũng không ngồi cuối.
`=>` Có `4.A_3 ^2 .3! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
Gọi `A:`" H/s lớp `C` không ngồi cạnh h/s lớp `B`"
`=>n(A)=144.2=288`
`=>P(A)=288/720=2/5`
`->bb D`