Tìm các số thực x, y sao cho ( x – 2 y ) + ( x + y + 4 ) . i = ( 2 x + y ) + 2 y i .
A. x = 3, y = 1
B. x = 3, y = -1
C. x = -3, y = -1
D. x = -3, y = 1
Tìm các số thực x, y sao cho: (1 - 2i)x + (1 + 2i)y = 1 + i
A. x = 1 4 , y = 3 4
B. x = 1 4 , y = - 3 4
C. x = - 1 4 , y = 3 4
D. x = - 1 4 , y = - 3 4
Ta có
(1 - 2i)x + (1 + 2i)y = 1 + i
<=> (x + y) + (2y - 2x)i = 1 + i
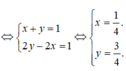
Chọn đáp án A.
tìm các số tự nhiên x, y tm : \(3^x+7=y^2\)
cho x, y, z là các số thực. cmr:
\(2xy-yz+xz\le x^2+y^2+z^2\)
cho x,y là các số thực ko âm t/m: x+y+z=2.Tìm giá trị nhỏ nhất của biểu thức:P= x^4+Y^4+Z^4
cho x,y là các số thực ko âm tm: x+y+z=2.Tìm giá trị nhỏ nhất của biểu thứcx^4+Y^4+Z^4 .
B tự c/m BĐT \(x^2+y^2+z^2\ge\frac{1}{3}\left(x+y+z\right)^2\)nhé.
Dấu " = " xảy ra \(\Leftrightarrow x=y=z\)
Áp dụng :
\(x^4+y^4+z^4\ge\frac{1}{3}.\left(x^2+y^2+z^2\right)^2\ge\frac{1}{3}.\left[\frac{1}{3}.\left(x+y+z\right)^2\right]^2=\frac{1}{27}.\left(x+y+z\right)^4=\frac{1}{27}.2^4=\frac{16}{27}\)
Dấu " = " xảy ra \(\Leftrightarrow x=y=z=\frac{2}{3}\)
KL:...
vận dụng bất đẳng thức x^2+y^2+z^2 \(\ge\) (x+y+z)^2/3
Áp dụng BĐT AM-GM ta có:
\(x^4+\frac{16}{81}+\frac{16}{81}+\frac{16}{81}\ge4.\sqrt[4]{x^4.\frac{16}{81}.\frac{16}{81}.\frac{16}{81}}=\frac{32}{27}x\)
Dấu " = " xảy ra \(\Leftrightarrow x^4=\frac{16}{81}\Leftrightarrow x=\frac{2}{3}\)
Tương tự:
\(y^4+\frac{16}{81}+\frac{16}{81}+\frac{16}{81}\ge4.\sqrt[4]{y^4.\frac{16}{81}.\frac{16}{81}.\frac{16}{81}}=\frac{32}{27}y\)
\(z^4+\frac{16}{81}+\frac{16}{81}+\frac{16}{81}\ge4.\sqrt[4]{z^4.\frac{16}{81}.\frac{16}{81}.\frac{16}{81}}=\frac{32}{27}z\)
Dấu " = " xảy ra \(\Leftrightarrow y^4=\frac{16}{81}\Leftrightarrow y=\frac{2}{3}\)
\(z^4=\frac{16}{81}\Leftrightarrow z=\frac{2}{3}\)
Cộng vế với vế của 3 BĐT trên ta có:
\(x^4+y^4+z^4+\frac{16}{81}.9\ge\frac{32}{27}\left(x+y+z\right)\)
\(\Leftrightarrow x^4+y^4+z^4\ge\frac{16}{27}\)
Dấu " = " xảy ra \(\Leftrightarrow x=y=z=\frac{2}{3}\)
Vậy Min \(x^4+y^4+z^4=\frac{16}{27}\)\(\Leftrightarrow x=y=z=\frac{2}{3}\)
Cho các số thực x,y,z thỏa mãn x+y+z=5 và xy+yz+zx=8. Tìm GTLN,GTNN của x,y,z
Tìm các số thực x,y,z thỏa mãn (x−1)^2 +|3y−1|+|z+2| = 0.
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\left|3y-1\right|\ge0\forall y\)
\(\left|z+2\right|\ge0\forall z\)
Do đó: \(\left(x-1\right)^2+\left|3y-1\right|+\left|z+2\right|\ge0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left(x,y,z\right)=\left(1;\dfrac{1}{3};-2\right)\)
Cho x, y là các số thực thoả mãn \(x\le1;x+y\ge3\)Tìm GTNN của \(P=3x^2+3xy+y^2\)
Hướng dẫn:
Ta có: \(x\le1\Rightarrow1-x\ge0\); \(x+y-3\ge0\)
Đặt: a = 1 - x và b = x + y - 3 ; với a; b không âm
=> y = a + b +2; x = 1 - a
Thế vào ta có: P = \(3\left(1-a\right)^2+3\left(1-a\right)\left(a+b+2\right)+\left(a+b+2\right)^2\)
Tìm min P với a; b không âm.
Tìm các số thực x,y thỏa mãn \(\hept{\begin{cases}x^2+y^2=9\\x^3+y^3=-27\end{cases}}\)
cho x,y là các số thực ko âm tm: x+y+z=2.Tìm giá trị nhỏ nhất của biểu thứcx^4+Y^4+Z^4
BÀY MINK CÁI