Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là:
A. 1
B. 2
C. 3
D. 4
PB
Những câu hỏi liên quan
Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là:
A. 1
B. 2
C. 3
D. 4
Chọn đáp án A
Hai đường tròn tiếp xúc với nhau thì có một điểm chung duy nhất
Đúng 0
Bình luận (0)
Cho hai đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả hai đường tròn trên tại B và C với B ∈ (O), C ∈ (O’).
b) Gọi M là trung điểm của BC. Chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O‘).
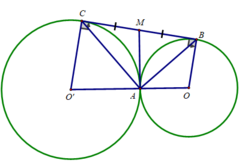
b) Ta có: M là trung điểm của cạnh huyền BC
⇒ MA = MB = MC
⇒ ΔMAB cân tại M ⇒ ∠(MAB ) = ∠(MBA )
Lại có: ΔOAB cân tại O ⇒ ∠(OAB ) = ∠(OBA )
⇒ ∠(MAB ) + ∠(OAB ) = ∠(MBA ) + ∠(OBA ) ⇔ ∠(MAO ) = ∠(MBO) = 90 0
⇒ MA là tiếp tuyến của (O)
Chứng minh tương tự: MA là tiếp tuyến của (O')
Vậy MA là tiếp tuyến chung của hai đường tròn (O) và (O')
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến của đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt (O) tại E và F. a. Kẻ tiếp tuyến chung của hai đường tròn. Chứng minh rằng . b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứng minh rằng .
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyếncủa đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt(O) tại E và F.a. Kẻ tiếp tuyến chung xAx của hai đường tròn. Chứng minh rằng EF//CD .b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứngminh rằng BAM90 độ .
Đọc tiếp
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến
của đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt
(O) tại E và F.
a. Kẻ tiếp tuyến chung xAx' của hai đường tròn. Chứng minh rằng EF//CD .
b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứng
minh rằng BAM=90 độ .
cho hai đường tròn (Ô,R) và( I,r) tiếp xúc trong tại tiếp điểm A ( với R r) d là tiếp tuyến chung của hai đường tròn tại tiếp điểm A . Dây AB của đường tròn (Ô,R) cắt đường tròn (I,r) tại M . Vẽ dây BC của đường tròn (O,R) sao cho BC tiếp xúc với đường tròn (I,r) tại K và tia BC cắt d tại S( B,O,C ko thẳng hàng) đoạn AC cắt đường tròn (I,r) tại N Cminh;a Hai đường thẳngMN vàSB song song với nhaub, tia AK là yia phân giác của góc BAC
Đọc tiếp
cho hai đường tròn (Ô,R) và( I,r) tiếp xúc trong tại tiếp điểm A ( với R > r) d là tiếp tuyến chung của hai đường tròn tại tiếp điểm A . Dây AB của đường tròn (Ô,R) cắt đường tròn (I,r) tại M . Vẽ dây BC của đường tròn (O,R) sao cho BC tiếp xúc với đường tròn (I,r) tại K và tia BC cắt d tại S( B,O,C ko thẳng hàng) đoạn AC cắt đường tròn (I,r) tại N
Cminh;
a Hai đường thẳngMN vàSB song song với nhau
b, tia AK là yia phân giác của góc BAC
cho hai đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả hai đường tròn trên tại B và C với B ∈ (O), C ∈ (O’).
a) Chứng minh tam giác ABC vuông
b) Gọi M là trung điểm của BC. Chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O‘).
https://diendantoanhoc.net/index.php?app=core&module=attach§ion=attach&attach_id=20602
Vào link này xem nhé
Học tốt!!!!!!!
cho tam giác ABC vuông tại A. Vẽ các đường tròn O và i đi qua A và tiếp xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng Minh
a) Các đường tròn O và i tiếp xúc với nhau
b) AM là tiếp tuyến chung của hai đường tròn O và i
c) tam giác OMI vuông
d) BC là tiếp tuyến của đường tròn ngoại tiếp tam giác OMI.
Hai đường tròn (O ; R) và (O' ; r) tiếp xúc ngoài với nhau. Gọi AB là tiếp tuyến chung của hai đường tròn, A∈(O),B∈(O′).
a) Tính độ dài AB.
b) Cho R=36cm,r=9cm. Tính bán kính của đường tròn (I) tiếp xúc với đường thẳng AB và tiếp xúc ngoài với hai đường tròn (O) và (O').
Bài 1. Cho hai điểm A(1;2) và B(3;4) và đường thẳng d: 3x+y+3=0.
1/ Viết phương trình các đường tròn \(\left(C_1\right)\) và \(\left(C_2\right)\) qua A, B và tiếp xúc với d.
2/ Viết phương trình tiếp tuyến chung (khác d) của hai đường tròn đó.