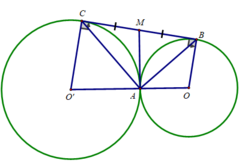
b) Ta có: M là trung điểm của cạnh huyền BC
⇒ MA = MB = MC
⇒ ΔMAB cân tại M ⇒ ∠(MAB ) = ∠(MBA )
Lại có: ΔOAB cân tại O ⇒ ∠(OAB ) = ∠(OBA )
⇒ ∠(MAB ) + ∠(OAB ) = ∠(MBA ) + ∠(OBA ) ⇔ ∠(MAO ) = ∠(MBO) = 90 0
⇒ MA là tiếp tuyến của (O)
Chứng minh tương tự: MA là tiếp tuyến của (O')
Vậy MA là tiếp tuyến chung của hai đường tròn (O) và (O')

