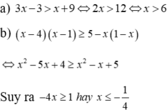Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số : x - 1 3 - 3 x + 5 2 ≥ 1 - 4 x + 5 6
PB
Những câu hỏi liên quan
giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số
\(\dfrac{x-1}{3}\)-\(\dfrac{3x+5}{2}\)≥1-\(\dfrac{4x+5}{6}\)
Ta có: \(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}\)
\(\Leftrightarrow2\left(x-1\right)-3\left(3x+5\right)\ge6-4x-5\)
\(\Leftrightarrow2x-2-9x-15-6+4x+5\ge0\)
\(\Leftrightarrow-3x\ge18\)
hay \(x\le-6\)
Đúng 0
Bình luận (0)
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
\(\dfrac{x-2}{2}+1\)≤\(\dfrac{x-1}{3}\)
\(\dfrac{x-2}{2}+1\le\dfrac{x-1}{3}\)
\(\Leftrightarrow\dfrac{3\left(x-2\right)}{6}+\dfrac{1.6}{6}\le\dfrac{2\left(x-1\right)}{6}\)
`<=> 3x - 6 + 6 <= 2x-2`
`<=> 3x <= 2x-2`
`<=> 3x -2x <= -2`
`<=> x <= -2`
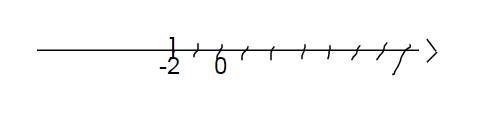
Đúng 2
Bình luận (2)
\(\dfrac{x-2}{2}\)+1≤\(\dfrac{x-1}{3}\)
<=>\(\dfrac{3x-6}{6}\)+\(\dfrac{6}{6}\)≤\(\dfrac{2x-1}{6}\)
<=>3x-6+6≤2x-1
<=>x<-1
Đúng 0
Bình luận (0)
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số x + 3 > 6
\(x+3>6\)
\(\Leftrightarrow x>6-3\)
\(\Leftrightarrow x>3\)
Biểu diễn trên trục số:
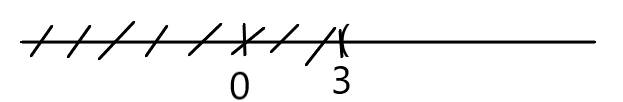
Đúng 0
Bình luận (0)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số: x - 1 < 3
x – 1 < 3
⇔ x < 3 + 1 (Chuyển vế và đổi dấu hạng tử -1)
⇔ x < 4
Vậy bất phương trình có nghiệm x < 4.

Đúng 0
Bình luận (0)
\(\dfrac{1-2x}{2}-\dfrac{x+1}{3}\le2\) . Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số
\(\Leftrightarrow3\left(1-2x\right)-2\left(x+1\right)< =6\)
=>3-6x-2x-2<=6
=>-8x+1<=6
=>-8x<=5
hay x>=5/8
Đúng 0
Bình luận (1)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:a)
3
x
−
3
x
+
9
;
b)
x
−
4
x
−
1
≥
5
−
x
1
−
x
Đọc tiếp
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3 x − 3 > x + 9 ; b) x − 4 x − 1 ≥ 5 − x 1 − x
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số. 2x-3(x+1)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:a)
(
2
x
+
3
)
(
2
x
−
1
)
(
2
x
−
5
)
2
b)
(
x
−
1
)
(
x
+
2
)
(...
Đọc tiếp
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) ( 2 x + 3 ) ( 2 x − 1 ) < ( 2 x − 5 ) 2
b) ( x − 1 ) ( x + 2 ) < ( x − 1 ) 2 + 3
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
a) 2x - 1 ≥ 5
b) x-2 /3 ≥ x - x-1 /2
a: 2x-1>=5
nên 2x>=6
hay x>=3
b: \(\dfrac{x-2}{3}>=x-\dfrac{x-1}{2}\)
=>2x-4>=6x-3(x-1)
=>2x-4>=6x-3x+3
=>2x-4>=3x+3
=>-x>=7
hay x<=-7
Đúng 2
Bình luận (0)
a.\(2x-1\ge5\)
\(\Leftrightarrow2x\ge6\)
\(\Leftrightarrow x\ge3\)
Vậy \(S=\left\{x|x\ge3\right\}\)
b.\(\dfrac{x-2}{3}\ge x-\dfrac{x-1}{2}\)
\(\Leftrightarrow\dfrac{2\left(x-2\right)}{6}\ge\dfrac{6x-3\left(x-1\right)}{6}\)
\(\Leftrightarrow2\left(x-2\right)\ge6x-3\left(x-1\right)\)
\(\Leftrightarrow2x-4\ge6x-3x+3\)
\(\Leftrightarrow-x\ge7\)
\(\Leftrightarrow x\le7\)
Vậy \(S=\left\{x|x\le7\right\}\)
Đúng 3
Bình luận (0)