Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng :
a) BDD’B’ là hình chữ nhật
b ) B B ’ ⊥ m p ( A B C D ) c ) m p ( A B B ’ A ’ ) ⊥ m p ( A B C D )
Cho hình hộp chữ nhật ABCD.A'B'C'D'.
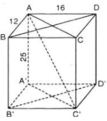
a,Chứng minh rằng tứ giác ADC'B' là hình chữ nhật.
b,Tính diện tích của hình chữ nhật ADC'B' biết: AB=12, AC'=29, DD'=16.
a: AD vuông góc DC
AD vuông góc D'D
=>AD vuông góc (DCC'D')
=>AD vuông góc DC'
Xét tứ giác ADC'B' có
AD//C'B'
AD=C'B'
góc ADC'=90 độ
=>ADC'B' là hình chữ nhật
b: AA'=16cm
AB=12cm
=>A'B=20cm
=>AB'=20cm
A'C'=căn 29^2-16^2=3*căn 65(cm)
A'B'=12cm
=>B'C'=căn A'C'^2-A'B'^2=21(cm)
S ADC'B'=21*20=420cm2
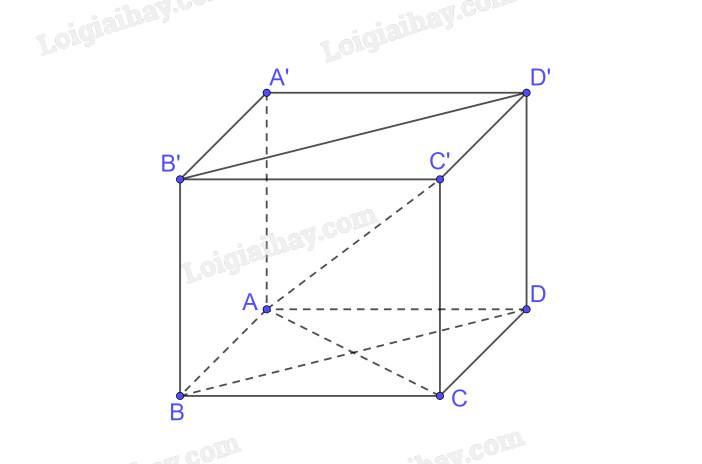
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒ 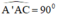
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Cho hình hộp chữ nhật ABCD. A'B'C'D'.
a) Chứng minh rằng (BDD′B′) \( \bot \) (ABCD).
b) Xác định hình chiếu của AC′ trên mặt phẳng (ABCD).
c) Cho AB = a, BC = b, CC′ = c. Tính AC′.
a) Ta có \(BB' \bot \left( {ABCD} \right);BB' \subset \left( {BDD'B'} \right) \Rightarrow \left( {BDD'B'} \right) \bot \left( {ABCD} \right)\)
b) A là hình chiếu của A trên (ABCD)
C là hình chiếu của C’ trên (ABCD) do \(CC' \bot \left( {ABCD} \right)\)
\( \Rightarrow \) AC là hình chiếu của AC’ trên (ABCD)
c) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \)
Xét tam giác AC’C vuông tại C có
\(A{C'^2} = C{C'^2} + A{C^2} = {c^2} + {a^2} + {b^2} \Rightarrow A'C = \sqrt {{a^2} + {b^2} + {c^2}} \)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’
a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Diện tích xung quanh:
2 x 3 x (5+7)= 72(cm2)
Thể tích của HHCN:
3 x 5 x 7 = 105(cm3)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’ a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Sxq=(5+7)*2*3=6*12=72cm2
V=5*7*3=105cm3
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Có AB = a, BC= b, CC'= c.
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A').
b) Tính độ dài đường chéo AC' theo a, b và c.
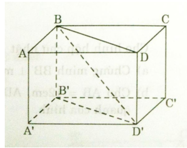
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
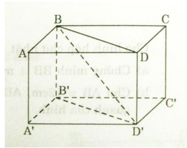
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
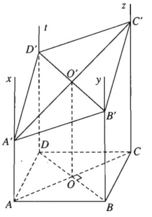
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)
Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.
Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′
b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.
c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.