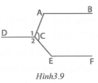
Trong hình 3.9, góc ACE bằng trung bình cộng của hai góc C 1 ^ và C 2 ^ , đồng thời cũng bằng trung bình cộng của hai góc A và E.
Biết C 1 ^ − C 2 ^ = A ^ − E ^ = 20 ° . Chứng tỏ rằng AB // CD và CD // EF
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
cho tam giác abc. chỉ dùng thước kẻ chia độ dài. hãy vẽ 1 góc bằng trung bình cộng của 2 góc B và C
Câu 39. Nếu hình bình hành ABCD có góc A = 530 thì
A.Góc D= 530 B. Góc B= Góc C = 530.
C. Góc C= 1270 D. Góc D= 1270
Câu 40. Hai cạnh kề của hình bình hành tỉ lệ với 1 và 2 và chu vi của hình bình hành bằng 30cm. Khi đó độ dài hai cạnh kề của hình bình hành là
A. 12cm và 18cm B. 5cm và 10cm
C. 15cm và 30cm D. 9cm và 18cm
Một hình tam giác vuông có trung bình cộng hai cạnh góc vuông là 44,5m và cạnh góc vuông này bằng 3/2 cạnh góc vuông kia .Tính diện tích hình tam giác vuông đó ?
tổng 2 góc vuông là:44,5*2=89(m)
cạnh góc vuông bé là:89:(3+2)*2=35,6(m)
cạnh góc vuông lớn là:89-35,6=53,4(m)
diên tich tam giác vuông là:(35,6*53,4):2=950,52(m2)
đ/s:950,52m2
1. Một hình thang có đáy lớn bằng 6,4cm; đáy bé bằng 340cm; chiều cao bằng trung bình cộng độ dài hai đáy. Tính DT hình thang.
2. Tính diện tích hình thang vuông ABCD có hai đáy là AB và DC, hai góc vuông là góc A và D, biết : AB = 1,5m ; DC = 27cm; AD = 18cm.
1. Diện tích hình thang là: 29998,24.
2. Diện tích hình thang là: 256,5.
Khẳng định nào sau đây là đúng ?
A.Trong hình bình hành các góc đối bù nhau
B. Trong hình bình hành hai góc kề 1 cạnh phụ nhau
C.Trong hình chữ nhật, 2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường
D. Trong hình bình hành hai đường chéo = nhau
Khẳng định nào sau đây là đúng ?
A.Trong hình bình hành các góc đối bù nhau
B. Trong hình bình hành hai góc kề 1 cạnh phụ nhau
C.Trong hình chữ nhật, 2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường
D. Trong hình bình hành hai đường chéo = nhau
cho hình bình thành ABCD a,biết AB=16cm , BC=12cm tính chu vi hình bình thành b,biết B=60 độ . tính các góc còn lại của hình bình thành ABCD c, Gọi E và F lần lượt ls trung điểm của AD và BC CM:tam giác ACE = tam giác CDF
Câu 54: Chọn khẳng định đúng.
A. Tứ giác có hai góc vuông là hình chữ nhật.
B. Hình bình hành có hai đường chéo bằng nhau.
C. Hình thoi có các góc bằng nhau.
D. Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Câu 55: Chọn khẳng định sai.
A. Chữ cái A có tâm đối xứng.
B. Chữ cái S có tâm đối xứng.
C. Đường tròn có tâm là tâm đối xứng.
D. Hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng.
Câu 56: Hình thoi có độ dài một đường chéo bằng độ dài một cạnh thì có một góc có số đo bằng
A. 300. B. 600.
B. 450. C. 750
Câu 57: Hình thoi có cạnh bằng 5cm, một đường chéo có độ dài bằng 6cm thì đường chéo còn lại có độ dài bằng
A. 7cm. B. 8cm.
B. 9cm. C. 10cm.
Câu 58: Hình chữ nhật có độ dài đường chéo bằng 10cm, độ dài một cạnh bằng 6cm thì độ dài của cạnh kề là
A. 8cm. B. 14 cm.
B. 4cm. C. 60cm
cho hình vuông ABC gọi E là điểm đối xứng củ A qua D
a) c/m tam giác ACE vuông cân
b) từ A kẻ AH vuông góc BE gọi zm và N lần lượt là trung điểm của AH và HE, C/m BMNC là hình bình hành
c) c/m M là trực tâm của tam giác ANB
d) c/m góc ANC bằng \(90_{_{ }}^o\)
a) Xét tam giác ACE có: DC vừa là trung tuyến vừa là đường cao của tam giác ACE
\(\Rightarrow\Delta ACE\)cân tại C (1)
Vì ABCD là hình vuông (gt)
\(\Rightarrow AC\)là tia phân giác của góc BCD (tc)
\(\Rightarrow\widehat{C1}=\widehat{C2}=\frac{1}{2}.\widehat{C}=\frac{1}{2}.90^0=45^0\)
Mà ACE là tam giác cân tại C(cmt)
\(\Rightarrow DC\)là phân giác của \(\widehat{ACE}\)
\(\Rightarrow\widehat{C1}=\widehat{DCE}=\frac{1}{2}\widehat{ACE}\)Mà \(\widehat{C1}=45^0\)
\(\Rightarrow45^0=\frac{1}{2}\widehat{ACE}\)
\(\Rightarrow\widehat{ACE}=90^0\left(2\right)\)
Từ (1) và (2) \(\Rightarrow ACE\)là tam giác vuông cân.
b) Xét tam giác AHE có:
M là trung điểm của AH (gt) , N là trung điểm của HE (gt)
\(\Rightarrow MN\)là đường trung bình tam giác AHE
\(\Rightarrow MN//AE\)và \(MN=\frac{1}{2}AE\)
\(\Rightarrow MN//AD\)và \(MN=AD\)( AD=DE=1/2AE)
Mà \(AD//BC\)và \(AD=BC\)( vì ABCD là hình vuông )
\(\Rightarrow MN//BC\)và \(MN=BC\)
Xét tứ giác BMNC có:
\(\hept{\begin{cases}MN//BC\left(cmt\right)\\MN=BC\left(cmt\right)\end{cases}\Rightarrow DMNC}\)là hình bình hành
c) Ta có: \(\hept{\begin{cases}AD\perp AB\\AD//MN\end{cases}\Rightarrow}MN\perp AB\)
Xét tam giác ANB có:
\(\hept{\begin{cases}MN\perp BA\left(cmt\right)\\AH\perp NB\left(gt\right)\end{cases}}\)và MN cắt AH tại M
\(\Rightarrow M\)là trực tâm tam giác ANB
d) Vì BMNC là hình bình hành (cmt)
\(\Rightarrow BM//NC\)(3)
Vì M là trực tâm tam giác ANB(cmt)
\(\Rightarrow BM\perp AN\)(4)
Từ (3) và (4) \(\Rightarrow NC\perp AN\)
\(\Rightarrow\widehat{ANC}=90^0\)
Cô ra có 1 bài mà hỏi hết luôn à, mách cô chép mạng nhá :>>>
:)))))
1. Một hình thang có đáy lớn bằng 8,4m ; đáy bé bằng 360cm; chiều cao bằng trung bình cộng độ dài hai đáy. Tính diện tích hình thang đó.
2. Tính diện tích hình thang vuông ABCD có hai đáy là AB và DC, hai góc vuông là góc A và góc D, biết : AB = 1,8m ; DC = 84cm ; AD = 4,8dm.
giúp mình với mình đang cần gấp.
1. Đổi 360cm=3,6m.
Chiều cao hình thang là:
(8,4+3,6):2=6(m)
S hình thang là:
\(\frac{\left(8,4+3,6\right)\cdot6}{2}=36\left(m^2\right)\)
đ/s
2. Theo đề bài và hình vẽ, ta thấy được:
AB: đáy lớn
CD: đáy bé
AD: chiều cao
Đổi: 1,8m=18dm
84cm=8,4dm
S hình thang vuông ABCD là:
\(\frac{\left(18+8,4\right)\cdot4,8}{2}=63,36\left(dm^2\right)\)
đ/s
1. Đổi 360cm=3,6m.
Chiều cao hình thang là:
(8,4+3,6):2=6(m)
S hình thang là:
8,4 + 3,6 · 6 = 36 m
( ) ( 2
)