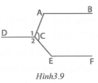
Tìm cách giải
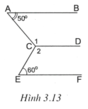
Trong hình vẽ đã có các cặp góc so le trong là A ^ và C 1 ^ ; E ^ và C 2 ^ . Muốn chứng tỏ AB // CD và CD // EF chỉ cần chứng tỏ A ^ = C 1 ^ và E ^ = C 2 ^ .
Trình bày lời giải
Ta có A C E ^ = C 1 ^ + C 2 ^ 2 ⇒ C 1 ^ + C 2 ^ = 2 A C E ^ .
Mặt khác C 1 ^ + C 2 ^ + A C E ^ = 360 ° nên 2 A C E ^ + A C E ^ = 360 ° ⇒ A C E ^ = 120 ° .
Do đó C 1 ^ + C 2 ^ = 360 ° − 120 ° = 240 ° mà C 1 ^ − C 2 ^ = 20 ° nên C 1 ^ = 130 ° ; C 2 ^ = 110 ° .
Ta có A C E ^ = A ^ + E ^ 2 ⇒ A ^ + E ^ = 2 A C E ^ = 240 ° .
Lại có A ^ − E ^ = 20 ° nên A ^ = 130 ° ; E ^ = 110 ° .
Ta có A ^ = C 1 ^ = 130 ° ⇒ A B / / C D ; E ^ = C 2 ^ = 110 ° ⇒ C D / / E F vì có cặp góc so le trong bằng nhau.
Vận dụng cặp góc đồng vị