Cho hàm số y = 2 x - 1 x - 1 có đồ thị là (C) . Gọi I l...

Hãy tham gia nhóm Học sinh Hoc24OLM

PB

Pham Trong Bach 28 tháng 2 2017 lúc 9:40

Cho hàm số y 2 x - 1 x - 1 có đồ thị là (C) . Gọi I là giao điểm hai tiệm cận của (C) . tồn tại điểm M( a; b) với; a; b nguyên dương thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI. Khi đó b-a ? A. 0 B. -1 C. 2 D. 1

Đọc tiếp

Cho hàm số y = 2 x - 1 x - 1 có đồ thị là (C) . Gọi I là giao điểm hai tiệm cận của (C) . tồn tại điểm M( a; b) với; a; b nguyên dương thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI. Khi đó b-a= ?

A. 0

B. -1

C. 2

D. 1

Lớp 12 Toán

H24

OtoriZu

13 tháng 12 2021 lúc 8:41

Bài 1: Cho hàm số y = (m - 1) x + m - 3(1) (với m là tham số, m≠1) a) Khi m = 0 hãy v ^ 2 đồ thị hàm số (L) trên mặt phẳng tọa độ Oxy b) Tim m để đồ thị hàm số (1) cắt trục tung tại điểm có tung độ bằng 1 c) Gọi A, B lần lượt là giao điểm của đồ thị hàm số (1) với hai trục tọa độ Ox, Oy. Tim m sao cho tam giác OAB cận.

Xem chi tiết

Lớp 9 Toán Chương II - Hàm số bậc nhất

KR

Kimian Hajan Ruventaren

25 tháng 4 2022 lúc 20:06

Cho hàm số $y=x^4-2mx^2+m$ có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến $\Delta$ với đồ thị (C) tại A cắt đượng tròn $\left(\lambda\right):x^2+\left(y-1\right)^2=4$ tạo thành 1 dây cung có độ dài nhỏ nhất

Xem chi tiết

Lớp 11 Toán Bài 5: Khoảng cách

NT

Nguyễn Lê Phước Thịnh CTV

2 tháng 7 2023 lúc 15:02

x^2+(y-1)^2=4

=>R=2 và I(0;1)

A(1;1-m) thuộc (C)

y'=4x^3-4mx

=>y'(1)=4-4m

PT Δsẽ là y=(4-m)(x-1)+1-m

Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)

Giả sử (Δ) cắt (λ) tại M,N

$MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}$

MN min khi d(I;(Δ)) max

=>d(I;(Δ))=IF

=>Δ vuông góc IF

Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)

=>vecto u=(1;4-4m)

=>1*3/4-(4-4m)=0

=>m=13/16

Đúng 0

Bình luận (0)

SD

Sơn Đàm

7 tháng 12 2021 lúc 16:57

Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .

Xem chi tiết

Lớp 12 Toán

LN

lee minh nhật

13 tháng 12 2023 lúc 15:20

Bài 9: Xác định hàm số y ax+b biÕta) Đồ thị của hàm số qua A(1;-1) và có hệ số góc là 2b) Đồ thị của hàm số // với đường thẳng y -3x + 2 và cắt trục tung tại điểm có tung độ bằng 1.Bài 10: Cho hàm số: y -x + 2.a) Vẽ đồ thị của hàm số trên.b)Gọi A, B là giao điểm của đồ thị hàm số với các trục tọa độ. Tính khoảng cách từ gốc tọa độ O đến đường thẳng AB.

Đọc tiếp

Bài 9: Xác định hàm số y= ax+b biÕt

a) Đồ thị của hàm số qua A(1;-1) và có hệ số góc là 2

b) Đồ thị của hàm số // với đường thẳng y =-3x + 2 và cắt trục tung tại điểm có tung độ bằng 1.

Bài 10: Cho hàm số: y = -x + 2.

a) Vẽ đồ thị của hàm số trên.

b)Gọi A, B là giao điểm của đồ thị hàm số với các trục tọa độ. Tính khoảng cách từ gốc tọa độ O đến đường thẳng AB.

Xem chi tiết

Lớp 9 Toán

NT

Nguyễn Lê Phước Thịnh CTV

13 tháng 12 2023 lúc 18:29

Bài 10:

a: loading...

b:

y=-x+2

=>y+x-2=0

=>x+y-2=0

Khoảng cách từ O đến đến đường thẳng AB sẽ bằng khoảng cách từ O đến (d): y=-x+2

=>Khoảng cách từ O đến đường thẳng AB là:

$d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot1+0\cdot1+\left(-2\right)\right|}{\sqrt{1^2+1^2}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}$

Bài 9:

a: Vì hệ số góc của hàm số y=ax+b là 2 nên a=2

=>y=2x+b

Thay x=1 và y=-1 vào y=2x+b, ta được:

$b+2\cdot1=-1$

=>b+2=-1

=>b=-3

vậy: y=2x-3

b: Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=-3x+2 nên $\left\{{}\begin{matrix}a=-3\\b\ne2\end{matrix}\right.$

Vậy: y=-3x+b

Thay x=0 và y=1 vào y=-3x+b, ta được:

$b-3\cdot0=1$

=>b-0=1

=>b=1

Vậy: y=-3x+1

Đúng 1

Bình luận (0)

AH

Akai Haruma Giáo viên

13 tháng 12 2023 lúc 19:35

Bài 9:

a. Hệ số góc của đths là $2$, tức $a=2$

ĐTHS đi qua điểm $A(1;-1)$ nên:

$-1=a.1+b$

$\Leftrightarrow -1=2.1+b\Rightarrow b=-3$
Vậy hàm số cần tìm là $y=2x-3$
b.

ĐTHS song song với $y=-3x+2$ nên $a=-3$

ĐTHS cần tìm cắt trục tung tại điểm có tung độ $1$, tức là nó đi qua điểm $(0;1)$

$\Rightarrow 1=a.0+b\Rightarrow b=1$

Vậy đths cần tìm là $y=-3x+1$

Đúng 0

Bình luận (0)

AH

Akai Haruma Giáo viên

13 tháng 12 2023 lúc 19:38

Bài 10:

a. Bạn chọn 2 điểm bất kỳ thuộc ĐTHS và nối lại sẽ được đồ thị hàm số cần tìm.

b.

$A\in Ox\Rightarrow y_A=0$

Có: $0=y_A=-x_A+2\Rightarrow x_A=2$. Vậy điểm $A$ có tọa độ $(2;0)$

$B\in Oy\Rightarrow x_B=0$

$y_B=-x_B+2=-0+2=2$. Vậy điểm $B$ có tọa độ $(0;2)$

Gọi $d$ là khoảng cách từ $O$ đến $AB$. Theo công thức hệ thức lượng trong tam giác vuông:

$\frac{1}{d^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{|x_A|^2}+\frac{1}{|y_B|^2}$

$=\frac{1}{2^2}+\frac{1}{2^2}=\frac{1}{2}$

$\Rightarrow d=\sqrt{2}$

Đúng 0

Bình luận (0)

PB

Pham Trong Bach

20 tháng 1 2019 lúc 17:31

Cho hàm số y x + 2 1 - x 2 . Xét các mệnh đề sau đây: (I). Hàm số có tập xác định D(-1;1). (II). Đồ thị hàm số có 2 đường tiệm cận ngang là y1 và y-1. (III). Đồ thị hàm số có 2 đường tiệm cận đứng là x1 và x-1...

Đọc tiếp

Cho hàm số y = x + 2 1 - x 2 . Xét các mệnh đề sau đây:

(I). Hàm số có tập xác định D=(-1;1).

(II). Đồ thị hàm số có 2 đường tiệm cận ngang là y=1 và y=-1.

(III). Đồ thị hàm số có 2 đường tiệm cận đứng là x=1 và x=-1.

(IV). Hàm số có một cực trị.

Số mệnh đề đúng là:

A.3

B.1

C.2

D.4

Xem chi tiết

Lớp 12 Toán

CT

Cao Minh Tâm

20 tháng 1 2019 lúc 17:33

Chọn A

Đk để hàm số xác định là: . Vậy mệnh đề đúng.

Do hàm số có tập xác định nên không tồn tại do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề sai.

Do nên đồ thị hàm số có đường tiệm cận đứng là và . Vậy đúng.

Ta có

Do bị đổi dấu qua nên hàm số có một cực trị. Vậy mệnh đề đúng.

Do đó số mệnh đề đúng là .

Đúng 0

Bình luận (0)

TT

Trần Như Đức Thiên

25 tháng 4 2023 lúc 21:01

I. Cho hàm số y x3 - 2x2 + x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C), biết rằng đồ thị này song song với đường thẳng y -5x + 17. II. Xét tính liên tục của hàm số sau: left{{}begin{matrix}dfrac{-x^2+2x+1}{-x-1}|khix-13-2x|khix1end{matrix}right.tại x0 1 III. Cho hình chóp S.ABCD có SA perp (ABCD), ABCD là hình chữ nhật. Chứng minh rằng BC perp (SAC). Giải giúp mình nhé. Mai mình thi HKII rồi. Cảm ơn các bạn rất nhiều.

Đọc tiếp

I. Cho hàm số y = x³ - 2x² + x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C), biết rằng đồ thị này song song với đường thẳng y = -5x + 17.

II. Xét tính liên tục của hàm số sau:

$\left\{{}\begin{matrix}\dfrac{-x^2+2x+1}{-x-1}|khix=-1\\3-2x|khix=1\end{matrix}\right.$tại x₀ = 1

III. Cho hình chóp S.ABCD có SA $\perp$ (ABCD), ABCD là hình chữ nhật. Chứng minh rằng BC $\perp$ (SAC).

Giải giúp mình nhé. Mai mình thi HKII rồi. Cảm ơn các bạn rất nhiều.

Xem chi tiết

Lớp 11 Toán Câu hỏi của OLM

LH

Lê Quang Huy

13 tháng 2 2020 lúc 22:11

Cho hàm số y=(m+1)x-2 có đồ thị là đường thẳng d. Tìm m để đồ thị hàm số d cắt đồ thị hàm số y=x+3 tại điểm có tung độ là 2.

Xem chi tiết

Lớp 9 Toán Câu hỏi của OLM

VH

Vũ Thúy Hằng

17 tháng 12 2021 lúc 22:10

giúp mk câu này vs ạ Cho hàm số y x có đồ thị là đường thẳng (d1). hàm số y - x + 3 có đồ thị là đường thẳng (d2).và hàm số y m x + 2 có đồ thị là đường thẳng (d3).a) Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ Oxy.b) Gọi giao điểm của (d1) và (d2) là A, giao điểm của (d2) và trục Ox là B. Tính diện tích tam giác AOB .c) Xác định điểm D thuộc đường thẳng (d1) và E thuộc (d2) sao cho hoành độ của chúng đều bằng 3.d) Tìm m để (d3) song song với (d1).e) Tìm m để ba đường...

Đọc tiếp

giúp mk câu này vs ạ

Cho hàm số y = x có đồ thị là đường thẳng (d₁).

hàm số y = - x + 3 có đồ thị là đường thẳng (d₂).

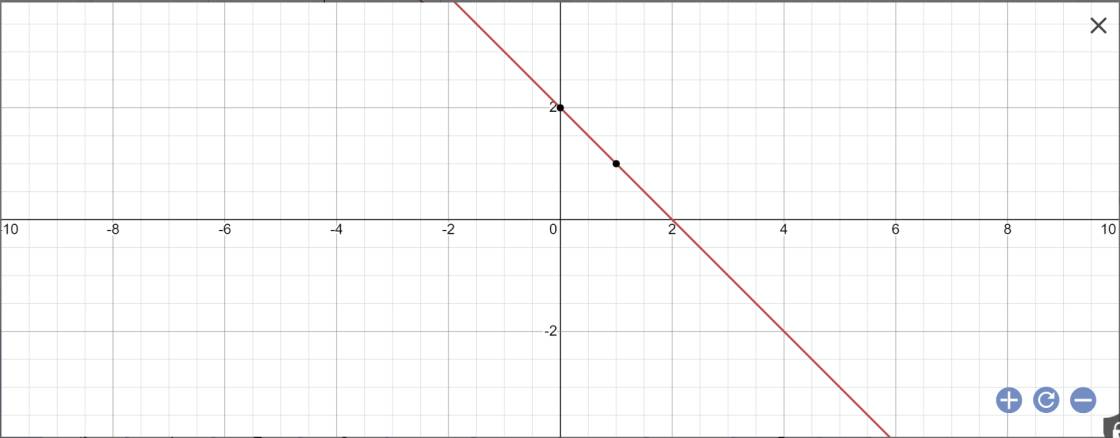
và hàm số y = m x + 2 có đồ thị là đường thẳng (d₃).

a) Vẽ (d₁) và (d₂) trên cùng mặt phẳng tọa độ Oxy.

b) Gọi giao điểm của (d₁) và (d₂) là A, giao điểm của (d₂) và trục Ox là B. Tính diện tích tam giác AOB .

c) Xác định điểm D thuộc đường thẳng (d₁) và E thuộc (d₂) sao cho hoành độ của chúng đều bằng 3.

d) Tìm m để (d₃) song song với (d₁).

e) Tìm m để ba đường thẳng đồng qui.

f) Chứng minh rằng (d₃) luôn đi qua một điểm cố định với mọi m.

g) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d₃) bằng 1

h) Tìm m để đường thẳng (d₃) cắt (d₂) tại điểm nằm ở góc phần tư thứ III.

Xem chi tiết

Lớp 9 Toán Chương II - Hàm số bậc nhất

NT

Nguyễn Lê Phước Thịnh CTV

18 tháng 12 2021 lúc 0:00

d: Để hai đường thẳng song song thì m=1

Đúng 0

Bình luận (1)

DB

Dân Chơi Đất Bắc=))))

13 tháng 5 2022 lúc 11:28

Trong mặt phẳng tọa độ Oxy,cho đồ thị hàm số y=f(x)=x²

1)Tính f(-1);f(3)

2)Cho A(-1;1),B(3;9) nằm trên đồ thị hàm số y=x².Gọi M là điểm thay đổi trên đồ thị hàm số y=x² và có hoành độ là m(-1<m<3).Tìm m để tam giác ABM có điện tích lớn nhất

P/s:Mọi người giúp em câu 2 với !!

Xem chi tiết

Lớp 9 Toán Ôn thi vào 10