a. Biên độ của dao động là: \(A=10\) (cm)

Tần số góc là: \(\omega=2\pi\) (rad/s)

Tần số là: \(f=\dfrac{\omega}{2\pi}=1\) (Hz)

Chu kì là: \(T=\dfrac{1}{f}=1\) (s)

b. Vận tốc và gia tốc cực đại lần lượt là:

\(v_{max}=\omega A=20\pi\) (cm/s)

\(a_{max}=\omega^2A=400\) (cm/s)

c. Phương trình vận tốc là:

\(v=20\pi\cos\left(2\pi t+\dfrac{\pi}{2}\right)\) (cm/s)

Dao động này có biên độ \(A=5cm\)

Tần số góc là \(5\pi\left(rad/s\right)\)

Chu kì \(T=\dfrac{2\pi}{\omega}=0,4s\)

Và tần số là: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)

⇒ Chọn B 

a) Biên độ A= 2 mm
Tần số góc ω = 180π (rad/s)
Chu kì \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{180\pi }} = \frac{1}{{90}}s\)
Tần số \(f = \frac{1}{T} = 90Hz\)

b) Phương trình vận tốc là:

v = −180π.2sin(180πt) = 360πsin(180πt) (mm/s)

Phương trình gia tốc là: a = −(180π)².2cos(180πt) (mm/s²)

Chọn A.

Giải thích:

Li độ: \(x=Acos\left(\omega t+\varphi\right)\)

Vận tốc: \(v=\omega Acos\left(\omega t+\varphi+\dfrac{\pi}{2}\right)=-\omega Asin\left(\omega t+\varphi\right)\)

Gia tốc: \(a=-\omega^2x=-\omega^2Acos\left(\omega t+\varphi\right)=\omega^2Acos\left(\omega t+\varphi+\pi\right)\)

Phương trình: \(x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)\)

a)Biên độ: \(A=2cm\)

Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)

Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)

Chiều dài quỹ đạo: \(L=2A=2\cdot2=4cm\)

b)Phương trình chất điểm:

Vận tốc: \(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)\)

Gia tốc: \(a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)\)

c)Em thay giá trị \(t=0,2s\) vào từng pt nhé.

Tại sao gia tốc lại bằng 250căn2  

Đáp án B

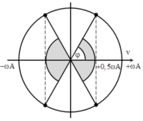
Vận tốc cực đại của con lắc  v max = ωA.

+ Khoảng thời gian trong một chu kì mà tốc độ của vật nhỏ không nhỏ hơn 0,5 v max  ứng với các góc quét được đánh dấu như hình vẽ.

→ Khoảng thời gian tương ứng là:

Δt = T 360 0 4 arccos 0 , 5 ωA ωA = 2 T 3

Chọn đáp án D

Đáp án B

Khi gia tốc của vật có độ lớn là 100 cm/ s 2 thì li độ của vật có độ lớn là x 0 . Suy ra

Thay vào công thức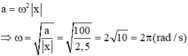

Do đó, tần số của dao động là f = ω 2 π  = 1 Hz