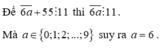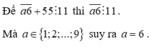Tìm giá trị của a để 101a chia hết cho 11
PB
Những câu hỏi liên quan
a)Tìm các giá trị của n để giá trị của biểu thức 2n^2 +3n+3 chia hết cho biểu thức 2n-1
b)Tìm các giá trị của n để giá trị của biểu thức25n^2 -97+11 chia hết cho biểu thức n-4
Tìm giá trị của a để tổng 6 a ¯ + 55 chia hết cho 11.
Tìm giá trị của a để tổng a 6 ¯ + 55 chia hết cho 11
Cho số 76a23
a) Tìm chữ số a để 76a23 chia hết cho 9
b) Trong các giá trị tìm được của a có giá trị nào làm cho số 76a23 chia hết cho 11 không?
76a23 chia hết cho 9
=> 7 + 6 + 2 + 3 + a chia hết cho 9
=> 18 + a chia hết cho 9
=> a = 0 hoặc a = 9
b) có nếu a = 9
~ hok tốt ~
Đúng 0
Bình luận (0)
a)
Để 76a23 chia hết cho 9 thì
7 + 6 + a + 2 + 3 chia hết cho 9
hay 18 + a chia hết cho a
=> a = { 0; 9 }
b)
Lần lượt thay a vào số đó ta thấy a = 9 thì 76a23 chia hết cho 11
Đúng 0
Bình luận (0)
a) Ta có: 76a23
Vì \(\overline{76a23}⋮9\Rightarrow7+6+2+3+a=18+a⋮9\)
\(\Rightarrow a\in\left\{0;9\right\}\)
b) Với a = 0 thì số \(\overline{76a23}=76023⋮̸\)\(11\)
Với a = 9 thì số \(\overline{76a23}=76923⋮11\)
Nhân xét: Dấu hiệu chia hết cho 11
\(a⋮11\)khi và chỉ khi tổng các chữ số hàng lẻ trừ đi tổng các chữ số hàng chẵn (hoặc ngược lại)
câu cuối chẳng hiểu lắm đâu, nhưng vẫn suy ra được, cố gắng hiểu nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho số 76a23
a, Tìm chữ số a để cho số 76a23 chia hết cho 9
b, Trong giá trị tìm được của a thì giá trị nào của a làm cho số 76a23 chia hết cho 11 ko?
76a23 chia hết cho 9
=> 7 + 6 + 2 + 3 + a chia hết cho 9
=> 18 + a chia hết cho 9
=> a = 0 hoặc a = 9
b) có nếu a = 9
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a,tìm số tự nhiên nhỏ nhất sao cho số đó chia cho 3 dư 1 chia cho 4 dư 2 chia cho 5 dư 3 chia cho 6 dư 4 và chia hết cho 11 ?
b, Tìm các giá trị nguyên của n để phân số A=3n+2/n-1 có giá trị là số nguyên ?
Bài 1: Làm tính chia a) (5x3-14x2+12x+8):(x+2) b) (2x4- 3x3+4x2+1): (x2-1)Bài 2: Tìm a để phép chia là phép chia hết 11x2 - 5x - a chia hết cho x + 5Bài 3: Tìm giá trị nguyên của n để giá trị của biểu thức 2n2 + n – 7 chia hết cho giá trị của biểu thức n – 2
Đọc tiếp
Bài 1: Làm tính chia
a) (5x3-14x2+12x+8):(x+2)
b) (2x4- 3x3+4x2+1): (x2-1)
Bài 2: Tìm a để phép chia là phép chia hết
11x2 - 5x - a chia hết cho x + 5
Bài 3: Tìm giá trị nguyên của n để giá trị của biểu thức 2n2 + n – 7 chia hết cho giá trị của biểu thức n – 2
Bài 3:
Ta có: \(2n^2+n-7⋮n-2\)
\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)
Đúng 0
Bình luận (0)
a,tìm giá trị của a để đa thức 3x2 + 7x + a +4 chia hết cho đa thức x - 5
b,tìm giá trị của b để đa thức 2x3 - 3x2 + x +b chia hết cho đa thức x + 2
Tìm nÎZ để giá trị của biểu thức n3 -2n2 + 3n + 3 chia hết cho giá trị của biểu thức n-1
b) Tìm a để đa thức x4 + 6x3 + 7x2 - 6x + a chia hết cho đa thức x2 + 3x - 1
\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
Đúng 1
Bình luận (0)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)
Đúng 1
Bình luận (0)