Cho hình vẽ dưới đây.
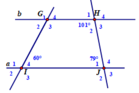 a. Chứng minh rằng a // b
a. Chứng minh rằng a // b
b. Tính số đo góc G 1 ^ , G 2 ^ , G 3 ^ , G 4 ^
Bài 2. Cho hình vẽ bên. a) Chứng minh rằng: aa’ // bb’. b) Tính số đo các góc (khác góc bẹt) có đỉnh Q |
|
a: Vì góc aMN=góc MNQ
nên aa'//bb'
b: góc PQN=180-100=80 độ=góc b'Qd'
góc b'Qd=d'QN=180-80=100 độ
cho hình vẽ a vuông góc với c, b vuông góc với c, góc aMP=35 độ và PNb=73 độ
a. chứng minh a // b
b. tính số đo góc MNP
Cho hình vẽ: Biết a // b.
a) Chứng tỏ AB vuông góc với đường thẳng b
b) Tính số đo góc: góc c1,góc d1
A) Ta có :a // b.
mà góc A vuông góc với a
=> AB vuông góc với đoạn thẳng b ( tính chất từ vuông góc tới song song )
b) câu này thì phải có 1 trong 2 góc thì mới tính được số đo góc chứ chỉ vẽ thế này là không đủ dữ liệu giải![]()
Cho hình vẽ dưới đây
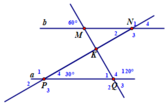 a. Chứng minh rằng a // b
a. Chứng minh rằng a // b
b. Tính số đo N 1 ^ ; N 2 ^ ; N 3 ^ ; N 4 ^
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
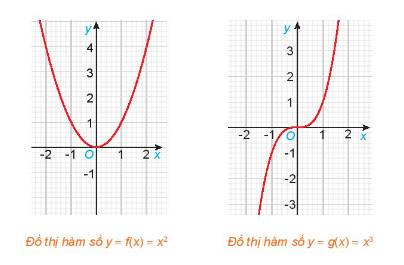
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ
Cho tam giác ABC có Ab = 1800 − 3Cb.
a) Chứng minh rằng Bb = 2Cb. Cho Bb = 800
, tính số đo các góc của tam giác.
b) Vẽ tia phân giác của góc B cắt AC tại E. Qua E kẻ đường song song với BC, cắt AB tại D. Chứng minh
rằng ED là tia phân giác của góc AEB.
mn giúp mình nha! mình cần vào ngày 22/08 r . 5 bn sớm nhất mình tick nhá
a, chứng minh aa'//bb' b, tính số góc m trên nx mặt phẳng bờ aa' chứa điểm n, vẽ tia mx // qp. tính số đo góc amx c, trên nữa mặt phẳng bờ aa' ko chứa điểm N vẽ ia mx' sao cho góc aMx = góc a'Mx chứng minh hai tia Mx và Mx' là 2 tia đối nhau
Cho \(\Delta ABC\) có G là trọng tâm . Vẽ đường thẳng d không giao \(\Delta ABC\) . Trên d gọi \(A',B',C',G'\) lần lượt là hình chiếu của \(A,B,C,G\) . Chứng minh rằng \(GG'=\dfrac{AA'+BB'+CC'}{3}\)
Lời giải:
Kéo dài $BG$ cắt $AC$ tại $K$. Kẻ $KK'\perp d$
Trên $BG$ lấy trung điểm $I$. Kẻ $II'\perp d$
Vận dụng công thức đường trung bình trong hình thang ta có:
Xét hình thang $BGG'B'$ có đtb $II'$ thì:
$II'=\frac{BB'+GG'}{2}(1)$
Xét hình thang $AA'C'C$ có đường trung bình $KK'$ thì:
$KK'=\frac{AA'+CC'}{2}(2)$
Xét hình thang $II'KK'$ có đường trung bình $GG'$ thì:
$GG'=\frac{II'+KK'}{2}(3)$
Từ $(1);(2);(3)$ suy ra:
$GG'=\frac{BB'+GG'+AA'+CC'}{4}$
$\Rightarrow GG'=\frac{AA'+BB'+CC'}{3}$
Ta có đpcm.
Cho hình vẽ bên biết : A2 + A3 + B1 = 240 độ và A1 = 120 độ
a, Chứng minh rằng a || b
b, Chứng minh rằng a vuông góc b