Cho tam giác ABC, A ^ = 90 ∘ , AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của H A B ^ cắt HB tại D. Tia phân giác của H A C ^ cắt HC tại E. Tính HE?
A. 4cm
B. 6cm
C. 9cm
D. 12cm
Cho tam giác ABC, A ^ = 90 ∘ , AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của H A B ^ cắt HB tại D. Tia phân giác của H A C ^ cắt HC tại E. Tính DH?
A. 4cm
B. 6cm
C. 9cm
D. 12cm
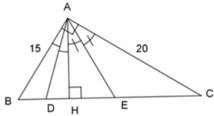
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 = > H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AD là phân giác của tam giác ABH nên: A B A H = B D D H ⇔ A B A H = B H − D H D H
⇔ 15 12 = 9 − D H D H ó 15DH = 108 – 12DH ó DH = 4cm
Đáp án: A
Cho tam giác ABC vuông tại A, có đường cao AH, AB=15cm, AC=20cm a) tính BC,AH b) vẽ tia phân giác AD của tam giác AHC (CD€ CH).CM tam giác ABD cân
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=12\left(cm\right)\)
b, Áp dụng HTL: \(HC=\dfrac{AC^2}{BC}=16\left(cm\right)\)
Vì AD là p/g nên \(\dfrac{HD}{DC}=\dfrac{AH}{AC}=\dfrac{3}{5}\Rightarrow HD=\dfrac{3}{5}DC\)
Mà \(DH+DC=HC=16\Rightarrow\dfrac{8}{5}DC=16\Rightarrow DC=10\left(cm\right)\)
\(\Rightarrow DH=6\left(cm\right)\\ \Rightarrow DB=BH+HD=25-16+6=15=AB\)
Do đó tg ABD cân tại B
Cho tam giác ABC, góc A=90°, đường cao AH, AB=15cm, AC=20cm a) C/m: CA²= CH.CB b) Kẻ AD là tia phân giác của góc BAC (D thuộc BC). Tính HD c) Trên tia đối của tia AC, lấy điểm I . Kẻ AK vuông góc với BI . C/m tam giác BHK đồng dạng với tam giác BIC d) Cho AI = 8cm. Tính Sbhk
a: Xét ΔABC vuông tại A có AH là đường cao
nên CA^2=CH*CB
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(AD=\dfrac{2\cdot15\cdot20}{15+20}\cdot cos45=\dfrac{60}{7}\sqrt{2}\)(cm)
AH=15*20/25=12(cm)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{12}{7}\left(cm\right)\)
c: ΔABI vuông tại A có AK là đường cao
nên BK*BI=BA^2=BH*BC
=>BK/BC=BH/BI
=>ΔBKH đồng dạng với ΔBCI
Cho ∆ABC vuông tại A, có AB=20cm, AC=15cm. Về đường cao AH (H thuộc BC)
a. Chứng minh: ∆HBA~∆ABC
b. Tính BC, AH, BH
c. Tia phân giác góc BAC cắt AC tại D. Tính tỉ số diện tích của 2 tam giác ABD và ACF
d. Trong ∆ABC kẻ phân giác AD (D thuộc BC). Trong ∆ADB kẻ phân giác DE (E thuộc AB) và trong ∆ADC kẻ phân giác DF (F thuộc AC). Chứng minh rằng EA/EB×DB/DC×FC/FA=1
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=25cm
AH=15*20/25=12cm
HB=20^2/25=16cm
HC=25-16=9cm
cho tam giác ABC, AH là đường cao, AM là phân giác. AB=15cm,BC=25cm,AC=20cm a. chứng minh tam giác ABC vuông b.tính AH,BH,CH c. tính MB,MB
\(a,AB^2+AC^2=15^2+20^2=625=25^2=BC^2\)
Vậy ABC là tam giác vuông tại A (pytago đảo)
\(b,\)Áp dụng HTL tam giác ABC vuông tại A, đường cao AH
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9\left(cm\right)\\CH=\dfrac{AC^2}{BC}=12\left(cm\right)\\AH=\sqrt{9\cdot12}=6\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Vì AM là phân giác nên \(\dfrac{MB}{MC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow MB=\dfrac{3}{4}MC\)
Mà \(MB+MC=BC=25\Rightarrow\dfrac{7}{4}MC=25\)
\(\Rightarrow MC=\dfrac{100}{7}\left(cm\right);MB=\dfrac{75}{7}\left(cm\right)\)
1, Cho tam giác ABC ( góc A=90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2=AB^2
2, Cho tam giác ABC( góc A=90 độ). phân giác AD, đường cao AH. biết BD=15cm, CD=20cm, tính BH, CH
3, Cho tam giác ABC( góc A=90 độ). AB=12cm, AC=16cm, phân giác AD, đường cao AH. tính HB,HC,HD
4, Cho tam giác ABC( góc A=90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH= 14 cm, HB/HC=1/4
giúp đỡ mình nhé, mình đang cần gấp
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
1) Cho tam giác ABC vuông tại A,đường phân giác AD.Tính độ dài AB,A C biết DB=15cm,DC=20cm
2) Cho tam giác ABC vuông tại A ,AB=15cm,AC=20cm,đường cao AH,tia phân giác của góc HAB cắt cạnh HB tại D ,tia phân giác của góc HAC cắt HC tại E.
a) Tính độ dài AH
b) Tính độ dài HD,HE
Bài 1:
Xét ΔABC có AD là phân giác
nen AB/BD=AC/CD
=>AB/3=AC/4
Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=35^2\)
=>k2=49
=>k=7
=>AB=21cm; AC=28cm
Cho tam giác ABC vuông tại A, có AB = 15cm, AC = 20cm, đường cao AH
a) Chứng minh tam giác ABC đồng dạng tam giác HBA
b) Tính BC, AH, HB, HC
c)Kẻ BD là đường phân giác của góc B cắt AH tại E. Tính AE, EH
a ) .
Xét 2 t/g vuông : ABC và HBA có:
góc B chung
do đó:
t/g ABC đồng dạng t/g HBA ( g - g )
b ) .
Áp dụng đl pytao vào t/g vuông ABC có :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\left(cm\right)\)
vi t/g ABC đồng dạng t/g HBA
=> \(\dfrac{AC}{HA}=\dfrac{BC}{AB}\Leftrightarrow\dfrac{20}{HA}=\dfrac{25}{15}\Rightarrow HA=20:\dfrac{25}{15}=12\left(cm\right)\)