Cho hàm số f(x) = e2+sin2x. Biết x 0 ∈ 0 ; π 2 là giá trị thỏa mãn f’(x0) = 0. Khi đó
A. x0 = π/2
B. x0 = π/3
C. x0 = 0
D. x0 = π/4
Tìm nguyên hàm F(x) của hàm số f(x)=sin2x, biết F π 6 = 0
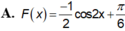
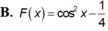
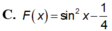
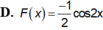
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 1 + sin 2 x với x ∈ R { - π 4 + k π , k ∈ } . Biết F(0)=1,F( π )=0, tính giá trị biểu thức P = F ( - π 12 ) - F ( 11 π 12 )
![]()
![]()
![]()
![]()
Tìm nguyên hàm F(x) của hàm số f x = sin 2 x , biết F π 6 = 0
A. F x = − 1 2 cos 2 x + π 6
B. F x = cos 2 x − 1 4
C. F x = sin 2 x − 1 4
D. F x = − 1 2 cos 2 x
Cho hàm số f(x) liên tục trên R Biết cận 0->pi/2 sin2x f(cos^2(x)) dx =1 Khi đó cân 0->1[2f(1-x) -3x^2+5]dx=?
Đề là cho \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx=1\)
Tính \(\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx\)
Đúng ko nhỉ?
Xét \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx\)
Đặt \(cos^2x=1-u\Rightarrow-2sinx.cosxdx=-du\) \(\Rightarrow sin2xdx=du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=\dfrac{\pi}{2}\Rightarrow u=1\end{matrix}\right.\) \(\Rightarrow I=\int\limits^1_0f\left(1-u\right)du=\int\limits^1_0f\left(1-x\right)dx\)
\(\Rightarrow\int\limits^1_0f\left(1-x\right)dx=1\)
\(\Rightarrow\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx=2\int\limits^1_0f\left(1-x\right)dx-\int\limits^1_0\left(3x^2-5\right)dx\)
\(=2.1-\left(-4\right)=6\)
Cho F(x) là một nguyên hàm của hàm số f x = 1 1 + sin 2 x với x ∈ ℝ \ - π 4 + k π , k ∈ Z . Biết F 0 = 1 , F π = 0 , tính giá trị biểu thức P = F - π 12 - F 11 π 12
A. P = 0
B. P = 2 - 3
C. P = 1
D. Không tồn tại P.
Chọn C.
Phương pháp : S
Cách giải : Ta có :
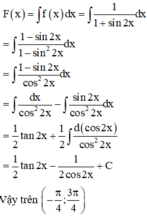
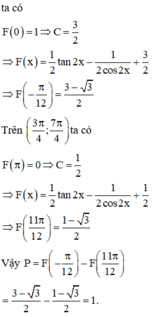
Cho f ( x ) = 4 m π + sin 2 x .Tìm để nguyên hàm của hàm số thỏa mãn F(0)=1 và F π 4 = π 8
A. -3/4
B. 3/4
C. -4/3
D. 4/3
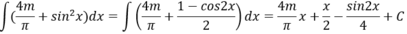
Vì F(0) = 1 nên C =1
F π 4 = π 8 nên tính được m = -3/4
Chọn A.
Một nguyên hàm F(x) của hàm số
f ( x ) = 2 x 3 = 3 x 2 + 1 - sin 2 x khi F(0)=1 là:
A. F x = 2 x 4 4 + 3 x 3 3 + x + 1 2 . cos 2 x + 1 2
B. F x = 2 x 4 4 - 3 x 3 3 + x + 1 2 . cos 2 x + 1 2
C. F x = 2 x 4 4 - 3 x 3 3 - x + 1 2 . cos 2 x + 1 2
D. F x = 2 x 4 4 - 3 x 3 3 + x + 1 2 . cos 2 x - 1 2
Một nguyên hàm F(x) của hàm số f ( x ) = 2 x 3 - 3 x 2 + 1 - sin 2 x khi F(0)=1 là:
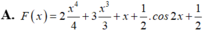
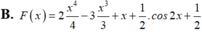
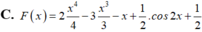
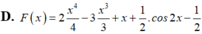
Cho hàm số f(x) = sin2x + 2cosx. Số điểm biểu diễn nghiệm của phương trình f’(x)=0 trên đường tròn lượng giác là:
A. 2
B. 3
C. 4
D. Vô số