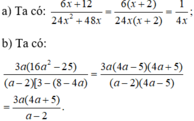Rút gọn các phân thức sau 2 a 2 - 2 a b a c + a d - b c - b d
PB
Những câu hỏi liên quan
Rút gọn các phân thức sau:a)
6
x
+
12
24
x
2
+
48
x
với
x
≠
−
2
và
x
≠
0
;b)
48
a...
Đọc tiếp
Rút gọn các phân thức sau:
a) 6 x + 12 24 x 2 + 48 x với x ≠ − 2 và x ≠ 0 ;
b) 48 a 3 − 75 a 3 ( a − 2 ) − ( a − 2 ) ( 8 − 4 a ) với a ≠ 5 4 và a ≠ 2 .
5.phân thức 4x/3 bằng với phân thức nào sau đây? A. -8x/6 b. 8x/6 c. 7x/6 D. 6/8x 6. Tìm điều kiện xác định của các phân thức sau A) x^2-1/x-2 b) 2x^2+3/x+1 7. Rút gọn các phân thức sau: A) 8x^3yz/24xy^2 b) 12x^4y^2z/x+1 8.thực hiện các phép tính sau: A) x^2+4/3x^2-6x + 5x+2/3x -4x/3x^2-6x
Câu 5: B
Câu 6:
a: ĐKXĐ: \(x-2\ne0\)
=>\(x\ne2\)
b: ĐKXĐ: \(x+1\ne0\)
=>\(x\ne-1\)
8:
\(A=\dfrac{x^2+4}{3x^2-6x}+\dfrac{5x+2}{3x}-\dfrac{4x}{3x^2-6x}\)
\(=\dfrac{x^2+4-4x}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)
\(=\dfrac{\left(x-2\right)^2}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)
\(=\dfrac{x-2+5x+2}{3x}=\dfrac{6x}{3x}=2\)
7:
\(\dfrac{8x^3yz}{24xy^2}\)
\(=\dfrac{8xy\cdot x^2z}{8xy\cdot3y}\)
\(=\dfrac{x^2z}{3y}\)
Đúng 2
Bình luận (0)
Bài 1 : ( 3 đ ) : Rút gọn các phân thức sau a)\(\dfrac{16x^2-1}{16x^2-8x+1}\) b)\(\dfrac{4x^2-4xy+y^2}{y^2-4x^2}\)
\(a.\)
\(\dfrac{16x^2-1}{16x^2-8x+1}\\ =\dfrac{\left(4x\right)^2-1}{\left(4x-1\right)^2}\\ =\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\\ =\dfrac{4x+1}{4x-1}\)
\(b.\)
\(\dfrac{4x^2-4xy+y^2}{-\left(4x^2-y^2\right)}\\ =-\dfrac{\left(2x-y\right)^2}{\left(2x-y\right)\left(2x+y\right)}\\ =\dfrac{-\left(2x-y\right)}{2x+y}\\ =\dfrac{y-2x}{y+2x}\)
Đúng 1
Bình luận (0)
a) Ta có: \(\dfrac{16x^2-1}{16x^2-8x+1}\)
\(=\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\)
\(=\dfrac{4x+1}{4x-1}\)
b) Ta có: \(\dfrac{4x^2-4xy+y^2}{y^2-4x^2}\)
\(=\dfrac{\left(2x-y\right)^2}{\left(y-2x\right)\left(y+2x\right)}\)
\(=\dfrac{\left(y-2x\right)^2}{\left(y-2x\right)\left(y+2x\right)}\)
\(=\dfrac{y-2x}{y+2x}\)
Đúng 1
Bình luận (0)
Rút gọn các phân thức sau :
a ) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}\) b ) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}\)
a ) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)
b ) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}\)
\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a-b+c}\)
Đúng 0
Bình luận (0)
a) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)
b) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{\left(a^2+2ab+b^2\right)-c^2}{\left(a^2+2ac+c^2\right)-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a+c-b}\)
Đúng 0
Bình luận (0)
Rút gọn phân thức sau\(\frac{a^2+b^2-c^2+2ab}{a^2+b^2+c^2+2ac}\)
\(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}\)
\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}\)
\(=\frac{\left(a+b-c\right)\left(a+b+c\right)}{\left(a+c-b\right)\left(a+c+b\right)}\)
\(=\frac{a+b-c}{a+c-b}\)
Bạn sai đề nên mik sửa và làm luôn nha
Đúng 0
Bình luận (0)
\(a^2+b^2-c^2+2ab\)
______________________
\(a^2+b^2+c^2+2ac\)
= \(a^2+b^2-c^2+2ab\) (Ở đây ta gạch a2,b2,c2,2a)
_____________________________
\(a^2+b^2+c^2+2ac\) (Ở đây ta cũng gạch a2,b2,c2,2a)
=> Kết quả cuối của biểu thức là: \(\frac{b}{c}\)
Tíck cho mình nha
Đúng 0
Bình luận (0)
Rút Gọn phân thức sau: {a^3(b^2-c^2)+b^3(c^2-a^2)+c^3(a^2-b^2)}/{a^2(b-c)+b^2(c-a)+c^2(a-b)}
Câu 2 Rút gọn các phân thức sau::(2 điểm )
a/ \(\dfrac{21x^2y^3}{24x^3y^2}\) b/ \(\dfrac{15xy^3\left(x^2-y^2\right)}{20x^2y\left(x+y\right)^2}\)
\(a,\dfrac{21x^2y^3}{24x^3y^2}=\dfrac{7y}{8x}\)
\(b,\dfrac{15xy^3\left(x^2-y^2\right)}{20x^2y\left(x+y\right)^2}=\dfrac{15xy^3\left(x-y\right)\left(x+y\right)}{20x^2y\left(x+y\right)^2}=\dfrac{3y^2\left(x-y\right)}{4x\left(x+y\right)}=\dfrac{3xy^2-3y^3}{4x^2+4xy}\)
Đúng 0
Bình luận (0)
a) Ta có: \(\dfrac{21x^2y^3}{24x^3y^2}\)
\(=\dfrac{21x^2y^3:3x^2y^2}{24x^3y^2:3x^2y^2}\)
\(=\dfrac{7y}{8x}\)
Đúng 0
Bình luận (0)
rút gọn các phân thức sau :
a) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}\)
b) \(\frac{a^3+b^3+c^3-3abc}{a^2+b^2+c^2-ab-bc-ca}\)
a, Gợi ý nà :3
a^2 + b^2 - c^2 +2ab = (a^2 + b^2 + 2ab) -c^2 = (a+b)^2 - c^2 = (a + b - c)(a + b + c)
a^2 - b^2 + c^2 + 2ac = (a + c)^2 - b^2 = (a + b + c)(a - b + c)
b. Gợi ý tiếp luôn nà :3
a^3 + b^3 + c^3 - 3abc
= (a^3 + b^3 +3a^2 x b + 3ab^2) - 3ab(a+b) -3abc + c^3
= (a+b)^3 + c^3 - 3ab(a+b+c)
= (a + b+ c)[(a+b)^2 - c(a+b) +c^2] - 3ab(a+b+c)
=(a+b+c)(a^2 + b^2 + c^2 -ac -bc + 2ab -3ab)
=(a+b+c)(a^2 + b^2 + c^2 - ab - bc -ca)
Rồi cứ thế rút gọn...
Học tốt nha bạn :3
\(\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+b+c\right)\left(a-b+c\right)}=\frac{a+b-c}{a-b+c}\)
\(\text{nhận xét: ta có hằng đẳng thức:}\)
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
đó đến đây bạn làm tiếp
b/\((\sum a^3)-3abc=(\sum a).(\sum a^2-\sum ab)\)\(\Rightarrow\)\(\frac{(\sum a^3)-3abc}{(\sum a^2-\sum ab)}=\frac {(\sum a).(\sum a^2-\sum ab)}{(\sum a^2-\sum ab)}=a+b+c\)
Xem thêm câu trả lời
Cho phân thức M=(a2+b2+c2)(a+b+c)2+(ab+bc+ca)2 / (a+b+c)2-(ab+bc+ca)
a,Tìm các giá trị của a,b,c để phân thức được xác định(tức để mẫu ≠0)
b,Rút gọn M
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
9
a
2
b
2
+
4
-
4
b
t
ạ
i
a
-
2
,
b
-
3
Đọc tiếp
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau: 9 a 2 b 2 + 4 - 4 b t ạ i a = - 2 , b = - 3
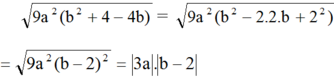
Thay a = -2, b = -√3 ta được:
|3(-2)|.|-√3 - 2| = 6(√3 + 2)
= 6(1,732 + 2) = 6.3,732
= 22,392
Đúng 0
Bình luận (0)