Cho hình thang vuông ABCD A ^ = D ^ = 90 0 , trong đó có C ^ = 45 0 , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3 c m 2
B. 8 c m 2
C. 4 c m 2
D. 6 c m 2
1, cho hình thang vuông ABCD có A = D = 90 độ , AB = AD =2 cm , CD= 4cm . tính B , C của hình thang.
2, cho hình thangg vuông ABCD có A = D =90 độ , CD = BC =2AB . Tính góc ABC.
\(2,\)
Kẻ BH vuông góc với CD tại H
Xét hai tam giác BDH và BCH:
+) BH là cạnh chung
+) Góc BHD = góc BHC = 90 độ
+) DH = CH
=> Tam giác BDH = tam giác HCH (c.g.c)
=> BD = BC
Khác: DC = BC
=> BC = CD = DB => Tam giác BCD đều => Góc C = 60 độ
Mà: AB // CD => Góc B + góc C = 180 độ => Góc B = góc ABC = 180 độ - 60 độ = 120 độ
Cho hình thang vuông ABCD có A ^ = D ^ = 90 ° , AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
A. 137 °
B. 136 °
C. 36 °
D. 135 °
Đáp án cần chọn là: D
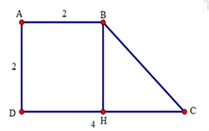
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .
Cho hình thang ABCD có góc A = D = 90°, B =60°, CD = 30cm, CA vuông góc với CB. Tính S hình thang.
dùng tỉ số lượng giác lần lượt tính được AD= \(10\sqrt{3}\) cm;AC= \(20\sqrt{3}\) cm;AB=20cm
do đó S hình thang\(=\frac{\left(ab+cd\right)\cdot ad}{2}=\frac{\left(20+30\right)\cdot10\sqrt{3}}{2}=\frac{500\sqrt{3}}{2}cm^2\)
Vậy....
Cách làm của bạn đúng rồi nhưng AB=40 cứ ko phải 20 nha
Cho hình thang ABCD có A=D=90 độ và 2 đường chéo vuông góc với nhau. Gọi AB=m, CD=n. Tìm diện tích bé nhất của hình thang ABCD
Diện tích hình thang này là 1 hằng số \(S=\dfrac{1}{2}\left(m+n\right)\sqrt{mn}\) nên không thể có giá trị lớn nhất hay nhỏ nhất gì đó được
Cho hình thang vuông ABCD có góc A = góc D = 90 độ, BC vuông góc BD, AB=2cm, CD=8cm.
a) Tính góc ABC và góc C
b) Tính diện tích hình thang ABCD.
a, Bạn chứng minh được \(\Delta ABD\infty\Delta BDC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow AB.DC=BD^2\Rightarrow2.8=BD^2\Rightarrow BD^2=16\Rightarrow BD=4\left(cm\right)\)(vì AB = 2cm , CD = 8 cm)
Ta có: \(\frac{BD}{CD}=\frac{4}{8}=\frac{1}{2}\)
Xét tam giác BDC vuông tại B có: BD = 1/2 CD nên \(\widehat{C}=30^0\)
ABCD là hình thang vuông(gt) \(\Rightarrow AB//CD\)
\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\) ( 2 góc trong cùng phía)
\(\Rightarrow\widehat{ABC}+30^0=180^0\) (do góc C = 30 độ)
\(\Rightarrow\widehat{ABC}=150^0\)
b, Áp dụng định lí Pitago vào tam giác ABD vuông tại A, tính được: \(AD=\sqrt{12}\left(cm\right)\)
Diện tích hình thang ABCD là:
\(\frac{\left(2+8\right).\sqrt{12}}{2}=5\sqrt{12}\left(cm^2\right)\)
Chúc bạn học tốt.
thang cho dung hoi nua
Cho hình thang vuông ABCD ( ∠A = ∠D = 90 độ ) AB = 4cm,AD = 15cm,BC = 17cm.Tính CD
Cho hình thang vuông ABCD(A=D=90).Có AB=1/2CD.Gọi H là hình chiếu của D trên AC M là trung điểm của HC.CMR:BMD=90
http://pitago.vn/question/cho-hinh-thang-vuong-abcd-goc-a-goc-d-90-do-co-ab-1-2-c-52909.html
Bạn vào trang này xem nhé!
Cho hình thang vuông ABCD, góc A= góc D=90 độ, AB=AD=2cm, BC=4cm
a,Tính các góc của hình thang
cho hình thang vuông abcd (a=d=90) có các điểm e,f thuộc cạnh ad sao cho góc bfc=90 chứng minh góc beo=90