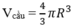Trong hình 8, có Ax // By. Chứng minh rằng A ^ + B ^ = A O B ^
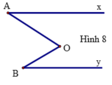
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz

a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
Cho nửa đường tâm O , đường kính AB = 4 cm . Kẻ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB . Gọi C là một điểm thuộc tia Ax . Kẻ tiếp tuyến CE với nửa đường tròn ( E là tiếp điểm ) , CE cắt By ở D .
a . Chứng minh rằng COOD = 90o ( Mình ko biết viết o ở trên không như trong sách ) .
b . Chứng minh rằng hình tam giác bằng chữ A ( ko biết viết hình ) AEB và hình tam giác bằng chữ A ( lại thế ) COD đồng dạng
c . Gọi I là trung điểm của CD . Vẽ đường tròn tâm I bán kính IC . Chứng minh rằng AB là tiếp tuyến của đường tròn ( i ) .
đ . Xác định vị trí của C trên tia Ax để có độ dài nhỏ nhất .
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
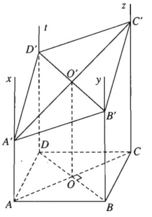
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)
Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.
Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′
b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.
c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)
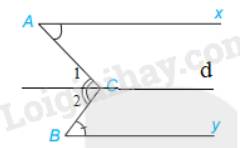
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)
Cho (O,R) đường kính AB vẽ 2 tiếp tuyến Ax By Lấy M thuộc O và M khác A B Tiếp tuyến tại M với O R cắt Ax By lần lượt tại C và D a chứng minh TG AMB vuông và CD =AC+BD b chứng minh AC.BD =R² c Gọi G là giáo điểm của OD với O Chứng minh rằng G là tâm đường tròn nội tiếp TG MDB Giúp mình a b với ạ
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
CD=CM+MD
mà CM=CA và DB=DM
nên CD=CA+DB
b:
OC là phân giác của góc MOA
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>ΔCOD vuông tại O
Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=R^2\)
c: Gọi H là giao điểm của DO và MB
Ta có: DM=DB
=>D nằm trên đường trung trực của MB(1)
Ta có: OM=OB
=>O nằm trên đường trung trực của MB(2)
Từ (1) và (2) suy ra OD là trung trực của MB
=>OD\(\perp\)MB tại H
Ta có: \(\widehat{GMH}+\widehat{OGM}=90^0\)(ΔGHM vuông tại H)
\(\widehat{DMG}+\widehat{OMG}=\widehat{DMO}=90^0\)
mà \(\widehat{OGM}=\widehat{OMG}\)
nên \(\widehat{GMH}=\widehat{DMG}\)
=>MG là phân giác của góc DMB
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DO là phân giác của góc MDB
Xét ΔMDB có
DH,MG là các đường phân giác
DH cắt MG tại G
Do đó: G là tâm đường tròn nội tiếp ΔMDB
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN.
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc ∠x'By.
C. Chứng minh điểm H nằm trên một đường tròn cố định.
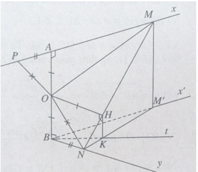
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
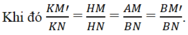
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
Hình 4.14 có A ^ = a ° ; B ^ = b ° a , b < 90 và A O B ^ = a ° + b ° . Chứng tỏ rằng Ax // By.

Ở trong góc AOB vẽ tia O t / / A x . Khi đó A O t ^ = A ^ = a ° (cặp góc so le trong).
Suy ra B O t ^ = b ° . Vậy B O t ^ = B ^ = b ° .
Do đó By // Ot (vì có cặp góc so le trong bằng nhau).
Vậy Ax // By (vì cùng song song với Ot)
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh AM ⋅ BN = R 2
c) Tính tỉ số S M O N S ∆ D B khi A M = R 2
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc  là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên  = 900
= 900
Tứ giác AOPM có:
![]()
Suy ra, tứ giác AOPM nội tiếp đường tròn.
![]()
Xét ∆ MON và ∆ APB có:
![]()
=> Hai tam giác MON và APB đồng dạng
b)
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
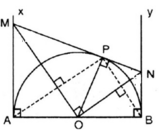
c) * Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
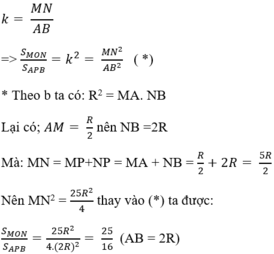
d) Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R.
nên thể tích khối cầu tạo ra là: