Phương trình sau có bao nhiêu nghiệm âm: x 4 − 2005 x 2 − 13 = 0
A. 0
B. 1
C. 2
D. 3
Phương trình sau đây có bao nhiêu nghiệm âm: x 6 + 2003 x 3 - 2005 = 0
A. 0
B. 1
C. 2
D. 6
Đặt t = x 3 thì phương trình x 6 + 2003 x 3 - 2005 = 0 trở thành
t 2 + 2003 t - 2005 = 0
Vì 1 . - 2005 < 0 suy ra phương trình ẩn t có 2 nghiệm trái dấu
Suy ra có phương trình đã cho có một nghiệm âm.
Đáp án cần chọn là: B
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
a) 15x2 + 4x - 2005 = 0; b) \(-\dfrac{19}{5}x^2-\sqrt{7}x+1890=0.\)
Khi phương trình ax2 + bx + c = 0 có a và c trái dấu thì ac < 0, suy ra –ac > 0; hơn nữa b2 ≥ 0. Do đó ∆ = b2 – 4ac > 0. Vậy phương trình có hai nghiệm phân biệt.
Áp dụng:
a) Phương trình 15x2 + 4x – 2005 = 0 có a = 15, c = -2005 trái dấu nhau nên phương trình có hai nghiệm phân biệt.
b) Phương trình x2 - √7x + 1890 = 0 có a =
và c = 1890 trái dấu nhau nên phương trình có hai nghiệm phân biệt.
2. Tìm giá trị của m để phương trình sau có 2 nghiệm cùng dấu. Khi đó 2 nghiệm mang dấu gì ? a) x - 2mx + 5m - 4= 0 (1) b) ma + mr +3 0 (2) 3. Cho phương trình: (m + 1)x2 + 2(m + 4)x + m+1 = 0 Tìm m để phương trình có: a) Một nghiệm b) Hai nghiệm phân biệt cùng dấu c) Hai nghiệm âm phân biệt 4. Cho phương trình (m - 4)x2 – 2(m- 2)x + m-1 = 0 Tìm m để phương trình a) Có hai nghiệm trái dấu và nghiệm âm có GTTÐ lớn hơn b) Có 2 nghiệm trái dấu và bằng nhau về GTTÐ c) Có 2 nghiệm trái dấu d) Có nghiệm kép dương. e) Có một nghiệm bằng 0 và một nghiệm dương.
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
có bao nhiêu cặp (a,b) để phương trình sau có nghiệm x∈R : (x-1)(x+2)(ax2+bx+2)≥0
Nguyên tắc xét dấu cơ bản: 1 đa thức (chính xác là biểu thức) luôn đổi dấu khi đi qua nghiệm bội lẻ và không đổi dấu khi đi qua nghiệm bội chẵn. Ở khoảng gần với dương vô cùng (nghĩa là các giá trị x rất lớn), dấu của đa thức luôn trùng với dấu của hệ số bậc cao nhất của biến.
Đặt \(f\left(x\right)=\left(x-1\right)\left(x+2\right)\left(ax^2+bx+2\right)\)
Do \(f\left(x\right)\) luôn có 2 nghiệm \(x=1;x=-2\) nên để \(f\left(x\right)\) không đổi dấu trên R thì đây phải là 2 nghiệm bội chẵn
\(\Rightarrow ax^2+bx+2=0\) có 2 nghiệm \(x=1;x=-2\)
Đồng thời theo nguyên tắc thứ 2 thì \(f\left(x\right)\ge0\) với mọi x khi \(a>0\)
Từ đó ta có hệ điều kiện: \(\left\{{}\begin{matrix}x_1+x_2=1-2=-\dfrac{b}{a}\\x_1x_2=1.\left(-2\right)=\dfrac{2}{a}\\a>0\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại a; b thỏa mãn yêu cầu đề bài
Số các giá trị nguyên âm của m để phương trình \(x^4+2x^3+3x^2+2x-m=0\) có nghiệm là bao nhiêu ?
Cho phương trình x 2 - (m + 1)x + m = 0. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có 2 nghiệm âm?
A. 0
B. 1
C. 2
D. Vô số
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
a ) 15 x 2 + 4 x − 2005 = 0 b ) − 19 5 x 2 − 7 x + 1890 = 0
a) Phương trình 15 x 2 + 4 x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
b) Phương trình 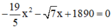 có
có 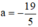 ; c = 1890 trái dấu
; c = 1890 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Các khẳng định sau đây đúng hay sai:
a. Phương trình 4 x - 8 + 4 - 2 x x 2 + 1 = 0 có nghiệm x = 2.
b. Phương trình x + 2 2 x - 1 - x - 2 x 2 - x + 1 = 0 có tập nghiệm S = {-2; 1}
c. Phương trình x 2 + 2 x + 1 x + 1 = 0 có nghiệm x = - 1
d. Phương trình x 2 x - 3 x = 0 có tập nghiệm S = {0; 3}
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 