Cho tứ diện S.ABCD ; gọi D; E; F lần lượt là trung điểm của AB ; BC; SA. Gọi H là giao điểm của AE và CD. Gọi giao tuyến của 2 mặt phẳng (SCD) và (BFC) là CI. SH và CI cắt nhau tại O. Tính tỉ số O H O S
A. 2 3
B. 1 2
C. 1 3
D. 2
Cho khối chóp tứ giác S.ABCD có đáy ABCD là hình thoi và SABC là tứ diện đều cạnh a. Thể tích V của khối chóp S.ABCD là
A. V = 2 2 a 3
B. V = 2 6 a 3
C. V = 2 4 a 3
D. V = 2 12 a 3
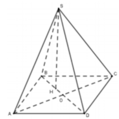
Gọi H là trọng tâm tam giác ABC. Vì S.ABC là tứ diện đều cạnh a nên S H ⊥ A B C hay S H ⊥ A B C D v à S A = S B = S C = A C = B C = a
Gọi O là giao điểm hai đường chéo hình thoi ABCD thì B H = 2 3 B O
Vì ABC đều có BO là trung tuyến nên \ B O = a 3 2

Xét tam giác SBH vuông tại H ta có

Diện tích hình thoi ABCD là
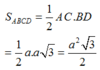
Thể tích khối chóp S.ABCD là
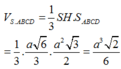 .
.
Chọn B.
Cho tứ diện ABCD có AB=2, CD=4 và các cạnh còn lại cùng bằng 6. Tính diện tích mặt cầu ngoại tiếp tứ diện S.ABCD
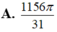
![]()
Cho tứ diện ABCD có AB=2; CD=4 và các cạnh còn lại cùng bằng 6. Tính diện tích mặt cầu ngoại tiếp tứ diện S.ABCD.
A. 1156 π 31
B. 1156 π 93
C. 47 π
D. 1280 π 93
Đán án C
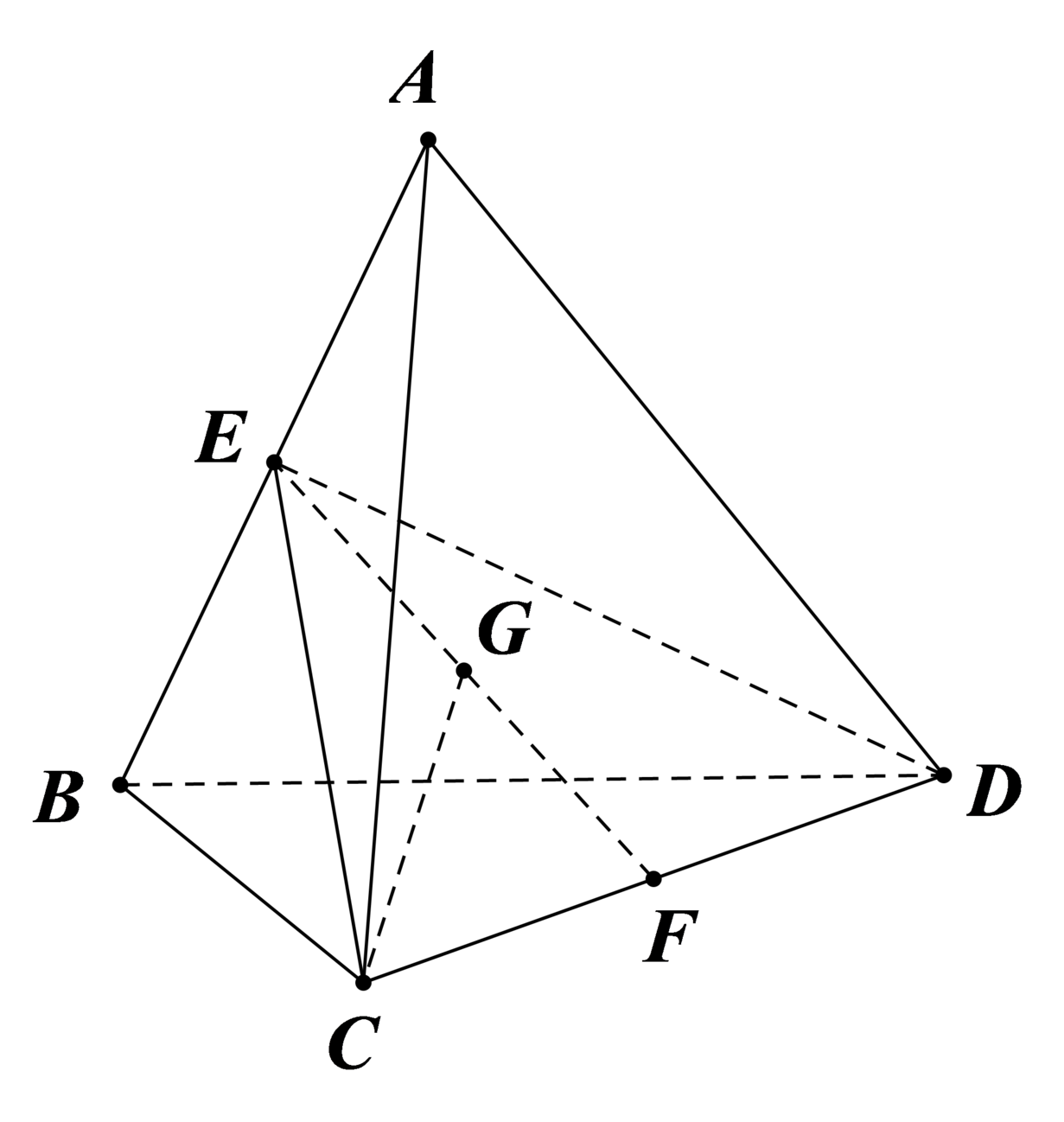
Gọi G là trung điểm của EF thì G chính là tâm mặt cầu ngoại tiếp tứ diện.
Ta có C E 2 = C B 2 + C A 2 2 − A B 2 4 = 6 2 + 6 2 2 − 2 2 4 = 35 ,
E F 2 = C E 2 − C F 2 = 35 − 2 2 = 31
⇒ G F = 31 2 ⇒ R = G C = G F 2 + C F 2 = 31 4 + 4 = 47 2 .
Vậy diện tích mặt cầu cần tính là:
S = 4 π R 2 = 4 π . 47 4 = 47 π .
Cho tứ diện S.ABCD có SA = AB = AC = a và AS, AB, AC vuông góc nhau từng đôi một. Tính diện tích mặt cầu ngoại tiếp tứ diện

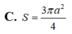
![]()
Cho khối chóp S.ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S.ABCD thành mấy khối tứ diện.
A. 2
B. 3
C. 4
D. 6
Chọn A.
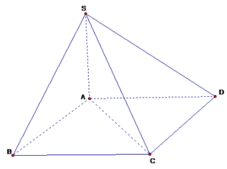
Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là S.ABC và S.ACD.
Cho khối chóp S.ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S.ABCD thành mấy khối tứ diện.
A. 4
B. 3
C. 2
D. 6
Chọn C
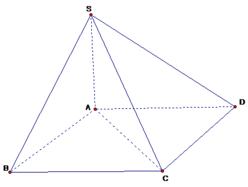
Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là : SABC,SACD
cho hình tứ gisác đều S.ABCD có SA=8cm, SB= 6cm
a, Tính thể tích của S. ABCD
b. Tính diện tích toàn phần, diện tích xung quanh của S.ABCD
Cho S.ABCD là một hình chóp có đáy ABCD là tứ giác lồi. Hình nào dưới đây không thể là thiết diện của hình chóp S.ABCD
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Chọn đáp án D
Hình chóp S.ABCD có 5 mặt nên thiết diện của hình chóp có tối đa 5 cạnh. Vậy thiết diện không thể là lục giác
cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 7cm và độ dài trung đoạn bằng 10cm.tính diện tích xung quanh của hình chóp tứ giác đều đó
Sxq=1/2*7*4*10
=2*70=140cm2
Cho hình chóp tứ giác đều S.ABCD có thể tích V, có O là tâm của đáy. Lấy M là trung điểm của cạnh bên SC. Thể tích khối tứ diện ABMO bằng
A. V 4
B. V 2
C. V 16
D. V 8