Xác định giá trị thực k để hàm số f x = x 2016 + x − 2 2018 x + 1 − x + 2018 khi x ≠ 1 k khi x = 1 liên tục tại điểm x=1
A. k = 1.
B. k = 2 2019 .
C. k = 2017 2018 2 .
D. 2016 2017 .
Xác định giá trị thực k để hàm số f x = x 2016 + x - 2 2018 x + 1 - x + 2018 , x ≠ 1 k , x = 1 liên tục tại x = 1.
A. k = 1
B. k = 2 2019
C. k = 2017 . 2018 2
D. 20016 2017 2019
Đáp án B
Để f(x) liên tục tại x = 1 thì lim x → 1 f ( x ) = f ( 1 ) . Ta có:
lim x → 1 f ( x ) = l i m x 2016 + x - 1 2018 x + 1 - x + 2018 = lim x → 1 2016 x + 1 1009 2018 x + 1 - 1 2 x + 2018 = 2 2019
Vậy k = 2 2019 .
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Xác định tất cả các giá trị thực của tham số m để phương trình |f(x)| = m có 6 nghiệm thực phân biệt.

A. 0 < m < 4
B. -1 < m < -2
C. 1 < m < 2
D. -1 < m < 2
Đáp án C.
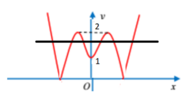
- Lấy đối xứng phần đồ thị hàm số y = f(x) nằm phía dưới trục hoành lên phía trên trục hoành ta được đồ thị hàm số y = |f(x)| (như hình bên). - Số nghiệm của phương trình |f(x)| = m là số giao điểm của đồ thị hàm số y = |f(x)| với đường thẳng y = m. Phương trình |f(x)| = m có 6 nghiệm thực phân biệt ⇔ 1 < m < 2.
Xác định giá trị thực k để hàm số f x = x 2016 + x − 2 2018 x + 1 − x + 2018 khi x ≠ 1 k khi x = 1 liên tục tại điểm x = 1
A. k = 1.
B. k = 2 2019 .
C. k = 2017 2018 2 .
D. k = 2016 2017 .
Đáp án B
Cách1: Tư duy tự luận
Hàm số liên tục tại điểm x = 1 khi lim x → 1 f x = f 1 .
Ta có f 1 = k và lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 .
= lim x → 1 x 2016 − x + 2 x − 1 2018 x + 1 + x + 2018 2018 x + 1 − x + 2018 2018 x + 1 + x + 2018
= lim x → 1 x x − 1 x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 x − 1
= lim x → 1 x x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 = 2015 + 2 .2 1019 2017
= 2 2019
Vậy để hàm số liên tục tại điểm x=1 khi k = 2 2019
Cách 2: Tư duy tự luận (tính giới hạn bằng công thức L’Hospital)
Ta có
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = lim x → 1 2016 x 2015 + 1 1009 2018 x + 1 − 1 2 x + 2018
= 2016 + 1 1009 2019 − 1 2 2019 = 2 2019
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .
Cách 3: Sử dụng máy tính cầm tay (casio và vinacal)
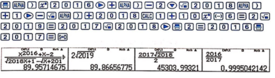
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = 2 2019 .
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .
Cho hàm số y=f(x) xác định trên R\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
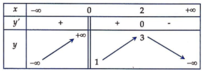
Tìm tất cả các giá trị của tham số thực m để phương trình f(x) -m=0
A. m ∈ 3 ; + ∞
B. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
C. m ∈ 3 ; + ∞
D. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
Đáp án A.
Ta có f x − m = 0 ⇔ f x = m . Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = m .Do đó để phương trình đã cho có nghiệm duy nhất thì đường thẳng y = m phải cắt đồ thị hàm số y = f x tại một điểm duy nhất. Khi đó m ∈ 3 ; + ∞ .
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Cho hàm số y = f(x) xác định trên R \ {1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
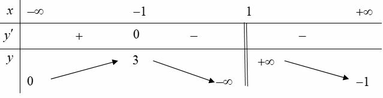
Số giá trị nguyên của tham số m để phương trình f(x) = m có 3 nghiệm thực phân biệt là
A. 0.
B. 3.
C. 2.
D. 1.
Cho hàm số y = f(x) xác định và liên tục trên [-2;2], có đồ thị của hàm số y= f'(x) như sau: Tìm giá trị x 0 để hàm số y=f(x) đạt giá trị lớn nhất trên [-2;2].
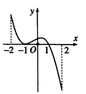
A. x 0 = 2
B. x 0 = -1
C. x 0 = -2
D. x 0 = 1
Cho hàm số y = f(x) xác định trên tập hợp ℝ \ 0 liên tục trên khoảng xác định có bảng biến thiên như sau. Tìm tất cả các giá trị của m để phương trình f(x) = m có hai nghiệm thực phân biệt.
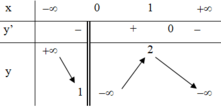
A. m = 2
B. m < 1
C. m = 2 hoặc m < 1
D. m ≤ 1 hoặc m = 2
Đáp án D
Từ bảng biến thiên ta thấy với m = 2 hoặc m ≤ 1 thì đồ thị hàm số y = f(x) cắt đường thẳng y = m tại 2 điểm phân biệt hay phương trình f(x) = m có 2 nghiệm phân biệt.
Cho hàm số y = f(x) xác định trên ℝ \ - 1 ; 1 , liên tục trên từng khoảng xác định và có bảng biến thiên như sau:
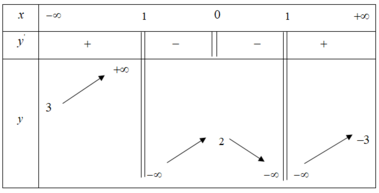
Tìm tất cả các giá trị thực của tham số của m để phương trình f(x) =3m có ba nghiệm phân biệt:
A. - 1 < m < 2 3
B. m < - 1
C. m ≤ - 1
D. m < - 3