Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Gọi M, N, P lần lượt là trung điểm AB, BC và SB. Mệnh đề nào sau đây là sai?
A. M N P / / S A C
B. B D ⊥ M N P
C. Góc giữa SC và BD là 60°
D. B C ⊥ M P
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với A B C D tại D lấy điểm S’ thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD. Gọi V 2 là thể tích khối chóp S.ABCD, tỉ số V 1 V 2 bằng
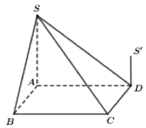
A. 1 2
B. 1 3
C. 2 2
D. 1 4
cho hình chóp s.abcd có đáy abcd là hình vuông cạnh a, \(SA=\sqrt{7}\) và vuông góc với đáy. lấy điểm M trên cạnh SC sao cho CM < a. gọi (C) là hình nón có đỉnh C, các điểm B, M, D thuộc mặt xung quanh, điểm A thuộc mặt đáy của hình nón. tính diện tích xung quanh của (C)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với tại D lấy điểm S’ thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD. Gọi V 2 là thể tích khối chóp S.ABCD, tỉ số V 1 V 2 bằng
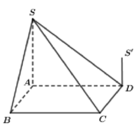
![]()
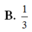
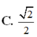
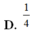
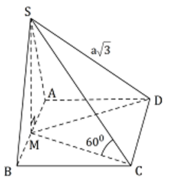
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD=a 3 SC tạo với mặt phẳng đáy (ABCD) một góc 60 o Thể tích khối chóp S.ABCD theo a là
A. 4 a 3 3
B. 3 a 3 10
C . 4 a 3 15 5
D . 2 a 3 15 3
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD = a 3 , SC tạo với mặt phẳng đáy (ABCD) một góc 60°. Thể tích khối chóp S.ABCD theo a là
A. 4 a 3 3
B. 3 a 3 10
C. 4 a 3 15 5
D. 2 a 3 15 3
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD = a 3 , SC tạo với mặt phẳng đáy (ABCD) một góc Thể tích khối chóp S.ABCD theo a là
A. 4 a 3 3 .
B. 3 a 3 10 .
C. 4 a 3 15 5 .
D. 2 a 3 15 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và có độ dài các cạnh AB = BC = 6, AD=12. Tam giác SAC vuông tại S. và có hình chiếu của S xuống (ABCD) là H thỏa mãn AC=34H. Gọi M, N lần lượt là trung điểm của SB,CD . Tinh tan (MN,(SAC))
Bạn ơi, bạn kiểm tra lại đề giúp mình nha, đoạn "...thỏa mãn AC=34H"
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a. Gọi I là trung điểm của cạnh AD, biết hai mặt phẳng (SBI); (SCI) cùng vuông góc với đáy và thể tích khối chóp S. ABCD bằng 3 15 a 3 5 . Tính góc giữa hai mặt phẳng (SBC); (ABCD).
A. 600
B. 300
C. 360
D. 450
Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Cách giải:
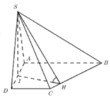
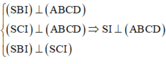
Kẻ IH
⊥
CD ta có: 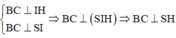
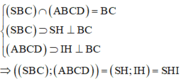
Ta có: 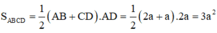
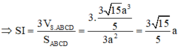
Gọi E là trung điểm của AB => EC = AD = 2a
![]()
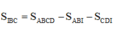
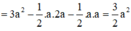
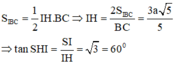

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB=AD=2a, CD=a. Gọi I là trung điểm của cạnh AD, biết hai mặt phẳng (SBI); (SCI) cùng vuông góc với đáy và thể tích khối chóp S. ABCD bằng 3 15 a 3 5 . Tính góc giữa hai mặt phẳng (SBC); (ABCD).
A. 60 0
B. 30 0
C. 36 0
D. 45 0