Số tiếp tuyến của đổ thị hàm số y = x + 2 2 x + 3 mà cắt trục hoành, trục tung lần lượt tại A và B sao cho ∆0AB cân là:
A. 0
B. 1
C. 2
D. 4
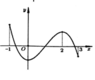
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-1;3] và có đổ thị như hình vẽ bên. Tiếp tuyến của đổ thị hàm số tại điểm x = 2 có hệ số góc bằng?
A. -1
B. 1
C. 0
D. 2
Đáp án C

Tại x = 2 là điểm cực trị nên tiếp tuyến song song với trục hoành do đó hệ số góc bằng 0.
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
Ta có : \(y=\dfrac{x-1}{x+1}\Rightarrow y'=\dfrac{\left(x+1\right)-\left(x-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\)
Giả sử d' là tiếp tuyến của đths đã cho . Do d' // d : y = \(\dfrac{x-2}{2}\)
\(\Rightarrow d'\) có HSG = 1/2 \(\Rightarrow\dfrac{2}{\left(x+1\right)^2}=\dfrac{1}{2}\Leftrightarrow4=\left(x+1\right)^2\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với x = 1 . PTTT d' : \(y=\dfrac{1}{2}\left(x-1\right)+0=\dfrac{1}{2}x-\dfrac{1}{2}\)
Với x = -3 . PTTT d' : \(y=\dfrac{1}{2}\left(x+3\right)+2=\dfrac{1}{2}x+\dfrac{7}{2}\)
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
y'=(x-1)'(x+1)-(x-1)(x+1)'/(x+1)^2=(x+1-x+1)/(x+1)^2=2/(x+1)^2
(d1)//(d)
=>(d1): y=1/2x+b
=>y'=1/2
=>(x+1)^2=4
=>x=1 hoặc x=-3
Khi x=1 thì f(1)=0
y-f(1)=f'(1)(x-1)
=>y-0=1/2(x-1)=1/2x-1/2
Khi x=-3 thì f(-3)=(-4)/(-2)=2
y-f(-3)=f'(-3)(x+3)
=>y-2=1/2(x+3)
=>y=1/2x+3/2+2=1/2x+7/2
Cho hàm số y=f(x) có đạo hàm liên tục trên tập R/ 2 và có đồ thị hàm số y=f’(x) như hình vẽ. Biết f 1 ≠ 10 f(3)=4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13
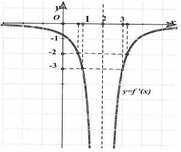
A. 2
B. 1
C. 0.
D. 3
Số tiếp tuyến của đổ thị hàm số y = x + 2 2 x + 3 mà cắt trục hoành, trục tung lần lượt tại A và B sao cho ∆0AB cân là
A. 0
B. 1
C. 2
D. 4
Đáp án B.
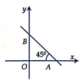
Δ O A B cân =>Tiếp tuyến tạo với Ox một góc 45 °
Hệ số góc của tiếp tuyến tại M x 0 ; y 0 ∈ ( C ) là y ' ( x 0 ) = ± tan 45 °
⇔ − 1 2 x 0 + 3 2 = 1 ( V N ) − 1 2 x 0 + 3 2 = − 1 ⇔ 2 x 0 + 3 = 1 2 x 0 + 3 = − 1 ⇔ x 0 = − 2 x 0 = − 1
-Với x 0 = − 1 ⇒ y 0 = 1 ⇒ Phương trình tiếp tuyến:
y = − 1 ( x + 1 ) + 1 ⇒ y = − x
-Với x 0 = − 2 ⇒ y 0 = 0 ⇒ Phương trình tiếp tuyến:
y = − 1 ( x + 2 ) ⇒ y = − x − 2
Tiếp tuyến của đồ thị hàm số y = - x + 1 3 x - 2 tại giao điểm của đồ thị hàm số với trục tung có hệ số góc là:
A. -1
B. 1/4
C. -5/4
D. -1/4
Tiếp tuyến của đồ thị hàm số y = − x + 1 3 x − 2 tại giao điểm của đồ thị hàm số với trục tung có hệ số góc là:
A. .-1
B. 1 4
C. − 5 4
D. − 1 4
Chọn D.
Phương pháp
Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x)

Do đó hệ số góc của tiếp tuyến tại tại giao điểm của đồ thị hàm số với trục tung là y ' 0 = − 1 4 .
Đề bài
Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
Cho hàm số y = x + 2 x - 2 tiếp tuyến của đồ thị hàm số kẻ từ điểm (-6;5) là:
A. y = - x - 1 ; y = 1 4 x + 7 2
B. y = - x - 1 ; y = - 1 4 x + 7 2
C. y = - x + 1 ; y = - 1 4 x + 7 2
D. y = - x + 1 ; y = - 1 4 x - 7 2
- Ta có:
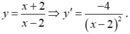
- Phương trình tiếp tuyến của đồ thị
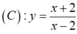
tại điểm M ( x 0 ; y 0 ) ∈ ( C ) với x 0 ≠ 2 là:
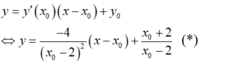
- Vì tiếp tuyến đi qua điểm (- 6; 5) nên ta có:
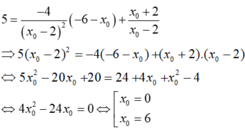
+ Với x 0 = 0 thay vào (*) ta có phương trình tiếp tuyến là: y = -x-1
+ Với x 0 = 6 thay vào (*) ta có phương trình tiếp tuyến là:
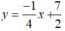
- Vậy có hai tiếp tuyến thỏa đề bài là:
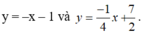
Chọn B.