Giúp mình câu f với ạ, mình cảm ơn
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
giúp mình câu d, e,f, h đi ạ, mình cảm ơn
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
giải giúp mình từ câu f đến hết ạ mình cảm ơn hứa rate 5 sao ạ
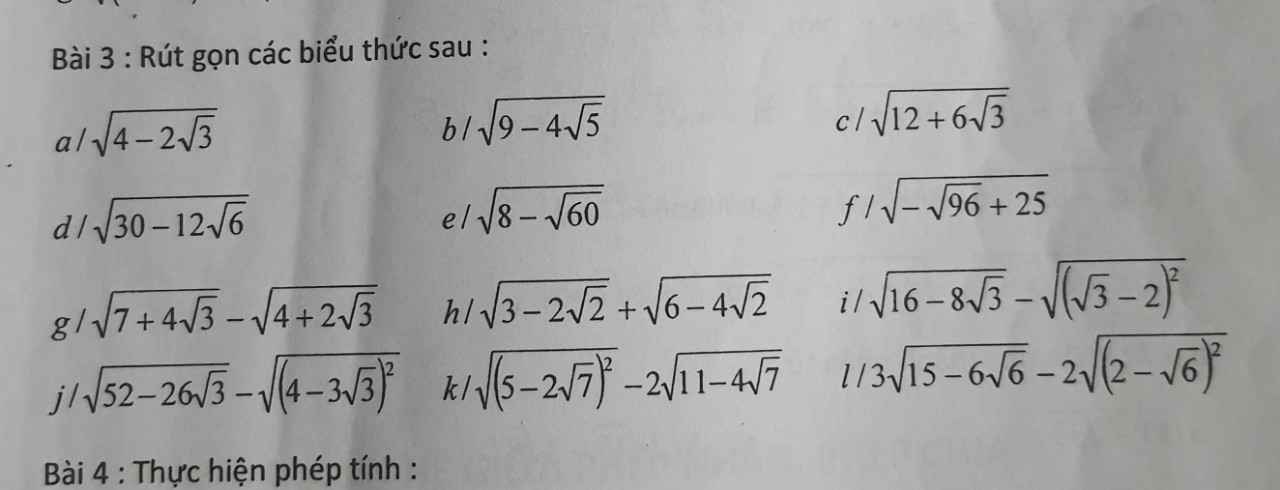
a) \(\sqrt{4-2\sqrt{3}}=\sqrt{3}-1\)
b) \(\sqrt{9-4\sqrt{5}}=\sqrt{10}-1\)
c) \(\sqrt{12+6\sqrt{3}}=3+\sqrt{3}\)
d) \(\sqrt{30-12\sqrt{6}}=3\sqrt{2}-2\sqrt{3}\)
e) \(\sqrt{8-\sqrt{60}}=\sqrt{5}-\sqrt{3}\)
f) \(\sqrt{-\sqrt{96}+25}=2\sqrt{6}-1\)
g: Ta có: \(\sqrt{7+4\sqrt{3}}-\sqrt{4+2\sqrt{3}}\)
\(=2+\sqrt{3}-\sqrt{3}-1\)
=1
h: Ta có: \(\sqrt{3-2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{2}-1+2-\sqrt{2}\)
=1
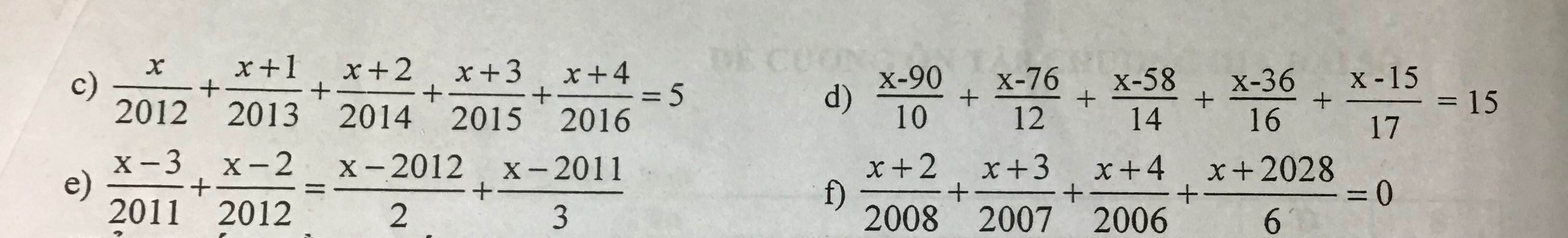 Giúp mình d,e,f với ạ !!!! Mình cảm ơn
Giúp mình d,e,f với ạ !!!! Mình cảm ơn
c: \(\Leftrightarrow\dfrac{x}{2012}-1+\dfrac{x+1}{2013}-1+\dfrac{x+2}{2014}-1+\dfrac{x+3}{2015}-1+\dfrac{x+4}{2016}-1=0\)
=>x-2012=0
hay x=2012
d: \(\Leftrightarrow\dfrac{x-90}{10}-1+\dfrac{x-76}{12}-2+\dfrac{x-58}{14}-3+\dfrac{x-36}{16}-4+\dfrac{x-15}{17}-5=0\)
=>x-100=0
hay x=100
giúp mình câu a b c e f nhé .Cảm ơn ạ!
b: =>(x+1)(x-1)-(x+3)(x-3)=2x^2+6x
=>2x^2+6x=x^2-1-x^2+9=8
=>2x^2+6x-8=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1(loại)
a: =>x^3+2x-2x(x^2+1)=0
=>x^3+2x-2x^3-2x=0
=>-x^3=0
=>x=0(nhận)
c: =>(x-2)(x+2)-(x+5)^2=x^2-8
=>x^2-4-x^2-10x-25=x^2-8
=>x^2-8=-10x-29
=>x^2+10x+21=0
=>(x+3)(x+7)=0
=>x=-3 hoặc x=-7
ai giúp mình với minh cảm ơn nhìu ạ. làm câu nào nào cũng được ạ mình cảm ơn 
giúp mình câu defgh với ạ, mình cảm ơn nhiều ạ.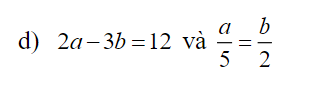
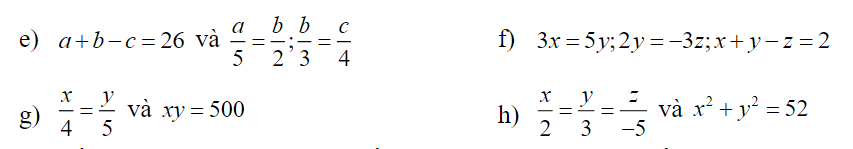
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a-3b}{2\cdot5-3\cdot2}=\dfrac{12}{4}=3\)
Do đó: a=15; b=6
d) Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a}{10}=\dfrac{3b}{6}=\dfrac{2a-3b}{10-6}=\dfrac{12}{4}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=3.5=15\\b=3.2=6\end{matrix}\right.\)
f) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=-\dfrac{z}{2}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{-z}{2}=\dfrac{x+y-z}{5+3+2}=\dfrac{2}{10}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}.5=1\\y=\dfrac{1}{5}.3=\dfrac{3}{5}\\z=\dfrac{1}{5}.\left(-2\right)=-\dfrac{2}{5}\end{matrix}\right.\)
g) \(\dfrac{x}{4}=\dfrac{y}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=20k^2=500\Rightarrow k=\pm5\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\\\left\{{}\begin{matrix}x=-20\\y=-25\end{matrix}\right.\end{matrix}\right.\)
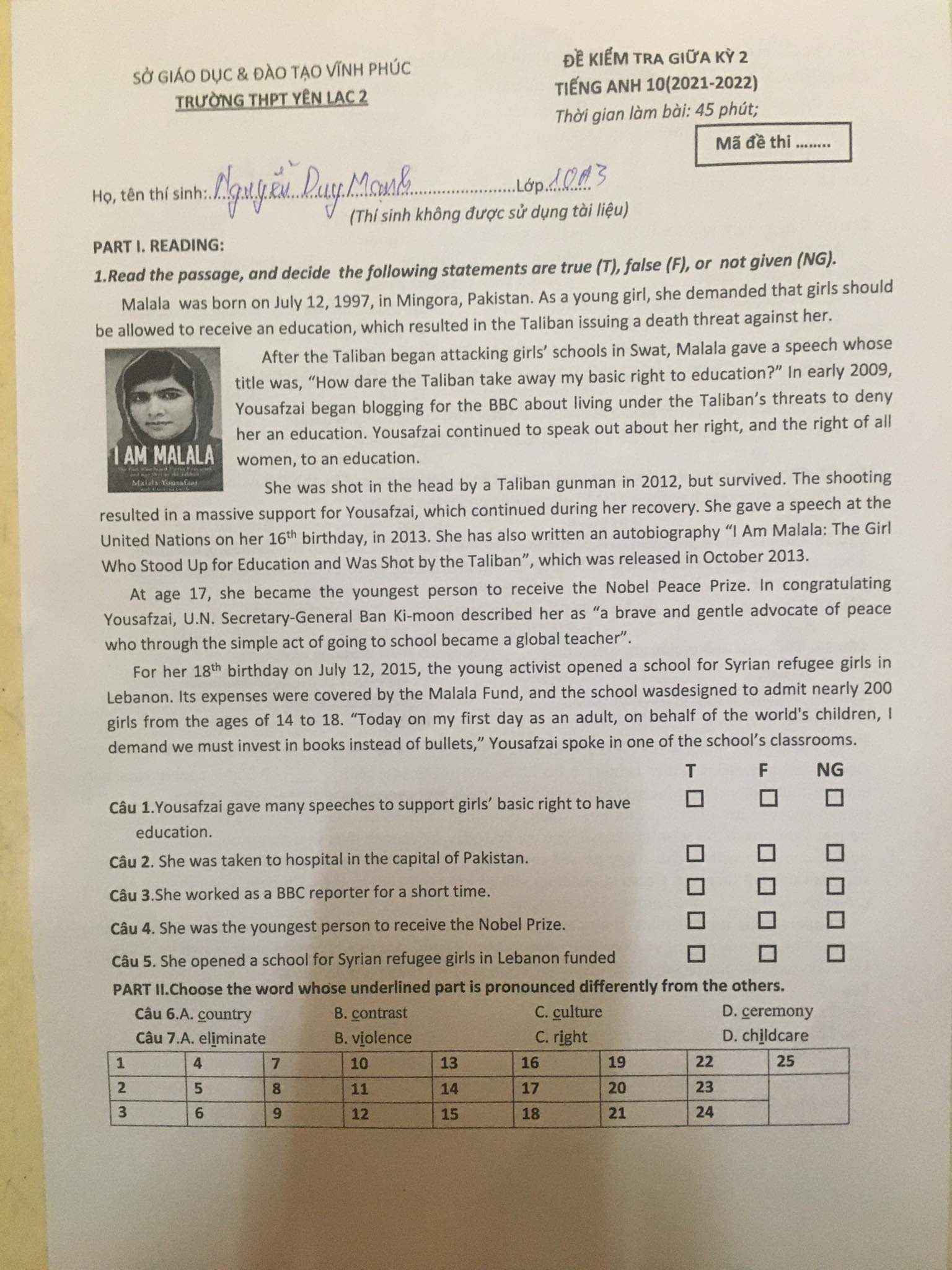
Các bạn giúp mik câu T F NG vs ạ
Mình xin cảm ơn !