1 TÌM x thuộcZ để A,B,C thuộc Z
A=x2+3:x+8
B=15x+8:7x+9
CV
Những câu hỏi liên quan
Giải phương trình sau đây :
a
)
8
(
3
x
-
2
)
-
14
x
2
(
4
–
7
x
)
+
15
x
b
)
(
3
x
–
1
)
(
x
–...
Đọc tiếp
Giải phương trình sau đây :
a ) 8 ( 3 x - 2 ) - 14 x = 2 ( 4 – 7 x ) + 15 x b ) ( 3 x – 1 ) ( x – 3 ) – 9 + x 2 = 0 c ) | x - 2 | = 2 x - 3 d ) x + 2 x - 2 - 1 x = 2 x x - 2
a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
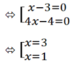
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
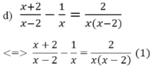
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2
Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1
Đúng 0
Bình luận (0)
Tìm x thuộc Z biết a) x ( x - 3) = 0; b) x ( x + 9) = 0 c) ( x + 1) ( x - 1) = 0 d) ( x - 13) ( x 2 + 8) = 0
giúp vs mk cần gấp lắm r
A=x+2/x+3 - 5/x2+x-6 + 1/2-x
a) tìm đkxd của A c) tìm x để A= -3/4
b) rút gọn A d) tìm x thuộc z để a thuộc z
e)tính giá trị cảu A khi x2-9=0
a: ĐKXĐ: \(x\notin\left\{-3;2\right\}\)
b: \(A=\dfrac{x^2-4-5+x+3}{\left(x-2\right)\left(x+3\right)}=\dfrac{x^2+x-6}{\left(x-2\right)\left(x+3\right)}=\dfrac{x+2}{x-2}\)
c: Để A=3/4 thì 4x-8=3x+6
=>x=14
d: Để A nguyên thì \(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{3;1;4;0;6;-2\right\}\)
Đúng 1
Bình luận (0)
Bài 1:
Cho A={x thuộc Z| x<-9}
Cho B={x thuộcZ|x<-4}
Cho C={x thuộc Z |>- -2}
mik ko quan tâm đc ko bn đéo quan tâm
1.TÌM x thuộc Z biết 10=10+9+8+7+6+5+4+3+2+1+x
2.tìm a,b,c thuộc Z biết a+b=11;b+c=3;c+a=2
3.cho x1+x2+x3+...+x51=0
và x1+x2=x3+x4=...=x50+x51=1
tính x50?
lưu ý trong 3. mấy con số sau x ko phải là để nhân mà là số thứ tự
cần lời giải lớp 6
teng kiu!
Tìm x thuộc Z để \(N=\frac{9}{\sqrt{x-5}}thuộcZ\)
TÌm số nguyên x để giá trị của phân thức sau là số nguyên:
a) A= ( x^4 - x^2 +2x - 1 ) / ( x^3 + 1 )
b) B= ( 15x + 8 ) / ( 7x + 9 )
Cho thức B= x2-x+2/x-3 với x ≠ 3
a) Tìm x để B<0
b) Tìm x thuộc Z để B thuộc Z:
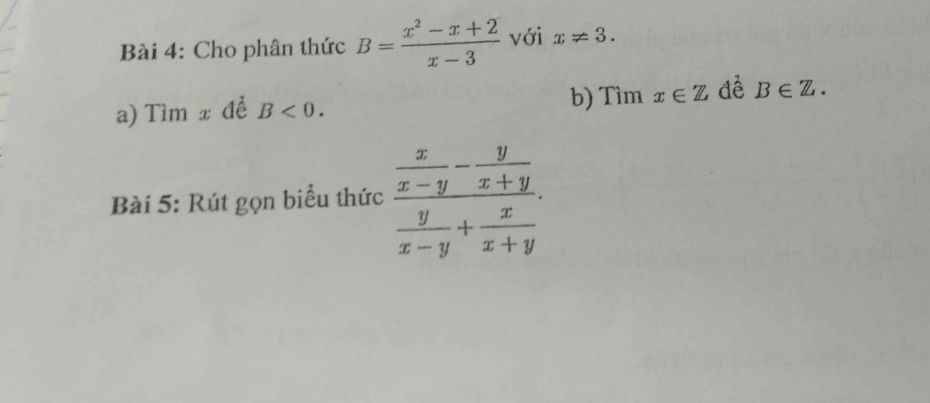
Bài 4:
a. Ta thấy: $x^2-x+2=(x-\frac{1}{2})^2+1,75>0$ với mọi $x$.
Do đó để $B=\frac{x^2-x+2}{x-3}<0$ thì $x-3<0$
$\Leftrightarrow x<3$
b.
$B=\frac{x(x-3)+2(x-3)+8}{x-3}=x+2+\frac{8}{x-3}$
Với $x$ nguyên, để $B$ nguyên thì $x-3$ phải là ước của 8.
$\Rightarrow x-3\in\left\{\pm 1; \pm 2; \pm 4; \pm 8\right\}$
$\Rightarrow x\in \left\{4; 2; 5; 1; -1; 7; 11; -5\right\}$
Đúng 1
Bình luận (0)
Bài 5:
\(\frac{\frac{x}{x-y}-\frac{y}{x+y}}{\frac{y}{x-y}+\frac{x}{x+y}}=\frac{\frac{x(x+y)-y(x-y)}{(x-y)(x+y)}}{\frac{y(x+y)+x(x-y)}{(x-y)(x+y)}}\)
\(=\frac{x(x+y)-y(x-y)}{y(x+y)+x(x-y)}=\frac{x^2+y^2}{x^2+y^2}=1\)
Đúng 0
Bình luận (0)
Tìm x thuộc Z để biểu thức có giá trị nguyên
a) A=\(\dfrac{3x+21}{x+4}\)
b) B=\(\dfrac{2x^3-7x^2+7x+5}{2x-1}\)
a)
ĐKXĐ: \(x\ne-4\)
Để A nguyên thì \(3x+21⋮x+4\)
\(\Leftrightarrow3x+12+9⋮x+4\)
mà \(3x+12⋮x+4\)
nên \(9⋮x+4\)
\(\Leftrightarrow x+4\inƯ\left(9\right)\)
\(\Leftrightarrow x+4\in\left\{1;-1;3;-3;9;-9\right\}\)
\(\Leftrightarrow x\in\left\{-3;-5;-1;-7;5;-13\right\}\)(nhận)
Vậy: Để A nguyên thì \(x\in\left\{-3;-5;-1;-7;5;-13\right\}\)
b) ĐKXĐ: \(x\ne\dfrac{1}{2}\)
Để B nguyên thì \(2x^3-7x^2+7x+5⋮2x-1\)
\(\Leftrightarrow2x^3-x^2-6x^2+3x+4x-2+7⋮2x-1\)
\(\Leftrightarrow x^2\left(2x-1\right)-3x\left(2x-1\right)+2\left(2x-1\right)+7⋮2x-1\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2-3x+2\right)+7⋮2x-1\)
mà \(\left(2x-1\right)\left(x^2-3x+2\right)⋮2x-1\)
nên \(7⋮2x-1\)
\(\Leftrightarrow2x-1\inƯ\left(7\right)\)
\(\Leftrightarrow2x-1\in\left\{1;-1;7;-7\right\}\)
\(\Leftrightarrow2x\in\left\{2;0;8;-6\right\}\)
hay \(x\in\left\{1;0;4;-3\right\}\)(nhận)
Vậy: \(x\in\left\{1;0;4;-3\right\}\)
Đúng 2
Bình luận (0)