Số giao điểm của đường thẳng d: y = 12x − 9 và parabol (P): y = 4 x 2 là:
A. 2
B. 1
C. 0
D. 3
B3:Tìm tọa độ giao điểm của Parabol (P) và đường thẳng (d) = phương pháp đại số trong trường hợp sau:
a) (P) y=2\(x^2\) và (d) y=5x-7
b)(P) y=12x\(^2\) và (d) y=3x+9
Giao điểm của đồ thị hàm số y = 2 x + 1 2 x - 1 và đường thẳng y = x + 2 là:
A. (1;3) và (-3/2; 1/2) B. (1;3) và (0;2)
C. (0; -1) và (-3/2; 1/2) D. (0; -1) và (0;2)
Đáp án: A.
Gợi ý: Thử trực tiếp vào phương trình
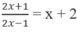
Cho parabol (P) :y= \(\dfrac{1}{2}\)x2 và đường thẳng (d): y= -x+m (x là ẩn,m là tham số)
a. tìm toạ độ giao điểm của parabol (P) với đường thẳng (d) khi m=4
a: Khi m=4 thì (d): y=-x+4
PTHĐGĐ là:
1/2x^2=-x+4
=>x^2=-2x+8
=>x^2+2x-8=0
=>(x+4)(x-2)=0
=>x=2 hoặc x=-4
Khi x=2 thì y=1/2*2^2=2
Khi x=-4 thì y=1/2(-4)^2=8
Cho hàm số y=1/2 x2 có đồ thị là parabol(P) và hàm số y=ax +b co dồ thị là đường thẳng (d)
a) vẽ parabol (P)
b)tìm a và b biết rằng đường thẳng (d) song song với đường thẳng y=x+5 và đi qua điểm A thuộc parabol (P) có hoành độ bằng -2
c) với a và b vừa tìm được ở câu trên , hãy tìm tọa độ các giao điểm của (P) và đường thẳng (d) bằng phép tính
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng (d): y=2(m-1)x+5-2m (m là tham số)
a) Vẽ đồ thị parabol (P).
b) Biết đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt. Gọi hoành độ giao điểm của đường thẳng (d) và parabol (P) là x1, x2. Tìm m để x+x=6
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4
1) Giải hệ phương trình sau:
$\left\{\begin{array}{l}\dfrac{2}{x-y}+\sqrt{y+1}=4 \\ \dfrac{1}{x-y}-3 \sqrt{y+1}=-5\end{array}\right.$.
2) Cho Parabol $(P): y=x^{2}$ và đường thẳng $(d): y=2(m-1) x-m^{2}+2 m$ ($m$ là tham số)
a) Tìm tọa độ giao điểm của Parabol $(P)$ và đường thẳng $(d)$ khi $m=2$.
b) Tìm $m$ để đường thẳng $(d)$ và Parabol $(P)$ cắt nhau tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ đối nhau.
1) ĐK \(\hept{\begin{cases}x\ne y\\y\ge-1\end{cases}}\)
Đặt \(\hept{\begin{cases}\frac{1}{x-y}=a\left(a\ne0\right)\\\sqrt{y+1}=b\left(b\ge0\right)\end{cases}}\)hệ phương trình đã cho trở thành
\(\hept{\begin{cases}2a+b=4\\a-3b=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+b=4\\2a-6b=-10\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=14\\2a+b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\end{cases}\left(tm\right)}\)
\(\Rightarrow\hept{\begin{cases}\frac{1}{x-y}=1\\\sqrt{y+1}=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=1\\y+1=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\y=3\end{cases}}\left(tm\right)\)
Vậy ...
1) Giải hệ phương trình $\left\{\begin{array}{l}2 \sqrt{x}+\dfrac{3}{y-1}=5 \\ 4 \sqrt{x}-\dfrac{1}{y-1}=3\end{array}\right.$
2) Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): y=x^{2}$ và đường thẳng $(d): y=m x-1$, với $m$ là tham số ($m \neq 0$)
a) Khi $m=3$, tìm tọa độ giao điểm của đường thẳng $(d)$ và parabol $(P)$.
b) Tìm tất cả các giá trị khác 0 của tham số $m$ để đường thẳng $(d)$ cắt parabol $(P)$ tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ thỏa mãn $x_{2}(x_{1}^{2}+1)=3$.
1) ĐK \(\hept{\begin{cases}x\ge0\\y\ne1\end{cases}}\)
Đặt \(\hept{\begin{cases}2\sqrt{x}=a\left(a\ge0\right)\\\frac{1}{y-1}=b\left(b\ne0\right)\end{cases}}\)hệ phương trình đã cho trở thành
\(\hept{\begin{cases}a+3b=5\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+6b=10\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=7\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}\left(tm\right)}\)
\(\Rightarrow\hept{\begin{cases}2\sqrt{x}=2\\\frac{1}{y-1}=1\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\left(tm\right)\)
Vậy ...
1,\(\left\{{}\begin{matrix}2\sqrt{x}+\dfrac{3}{y-1}=5\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\) ĐKXĐ:x≥o,y≠1
⇔\(\left\{{}\begin{matrix}4\sqrt{x}+\dfrac{6}{y-1}=10\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-1}=7\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\4\sqrt{x}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\left(TM\right)\)
vậy hpt đã cho có nghiệm duy nhất (x,y)=(1,2)
2,a, xét pthđgđ của (d) và (p) khi m=3:
x\(^2\)=3x-1⇔\(x^2-3x+1=0\)
Δ=(-3)\(^2\)-4.1.1=5>0
⇒pt có 2 nghiệm pb
\(x_1=\dfrac{3+\sqrt{5}}{2}\) ,\(x_2=\dfrac{3-\sqrt{5}}{2}\)
thay x=x\(_1\)=\(\dfrac{3+\sqrt{5}}{2}\) vào hs y=x\(^2\) ta được:
y=(\(\dfrac{3+\sqrt{5}}{2}\))\(^2\)=\(\dfrac{14+6\sqrt{5}}{4}\)⇒A(\(\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}\))
thay x=x\(_2\)=\(\dfrac{3-\sqrt{5}}{2}\) vào hs y=x\(^2\) ta được:
y=\(\left(\dfrac{3-\sqrt{5}}{2}\right)^2=\dfrac{14-6\sqrt{5}}{4}\)⇒B(\(\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}\))
vậy tọa độ gđ của (d) và (p) là A(\(\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}\)) và B (\(\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}\))
b,xét pthđgđ của (d) và (p) :
\(x^2=mx-1\)⇔\(x^2-mx+1=0\) (*)
Δ=(-m)\(^2\)-4.1.1=m\(^2\)-4
⇒pt có hai nghiệm pb⇔Δ>0
⇔m\(^2\)-4>0⇔m>16
với m>16 thì pt (*) luôn có hai nghiệm pb \(x_1,x_2\)
theo hệ thức Vi-ét ta có:
(I) \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=1\end{matrix}\right.\)
\(x_1,x_2\) TM \(x_2\)(x\(_1\)\(^2\)+1)=3
⇒\(x_2.x_1^2\)+\(x_2\)=3⇔\(x_2.x_1.x_1+x_2=3\)⇔(\(x_2.x_1\))(\(x_1+x_2\))=3 (**)
thay (I) vào (**) ta được:
1.m=3⇔m=3 (TM m≠0)
vậy m=3 thì (d) cắt (p) tại hai điểm pb có hoanh độ \(x_1.x_2\) TM \(x_2\)(\(x_1^2+1\))=3
BÀI 3:Xác định tham số m để hàm số y=(m^2 - 4)x-5 nghịch biến
Xác định tham số m để hàm số y=(m^2 - 1)x+2 đồng biến với mọi x>0
BÀI 6 Cho đường thẳng (d) y=-x+2 và parabol P y=1/2.x^2
a)tìm giá trị m để điểm M(m;m-1) nằm trên (d).Với m vừa tìm được chứng tỏ điểm M không thuộc P
b) vẽ P và (d) trên cùng mặt phẳng tọa độ và tìm tọa độ giao điểm của
chúng
BÀI 4:
TRONG mặt phẳng tọa độ Oxy , cho parabol P: y=-x^2
a) vẽ đồ thị P
b) gọi A và B là hai điểm thuộc P có hoành độ lần lượt là 1 , -2 .Lập phuơng trình đường thẳng AB
c) tìm phương trình đường thẳng (d) song song với đường thẳng AB và tiếp xúc với P
hết hạn khỏi giải nhé mỏ vịt đi bơi đi
Bài 3:
Đặt \(a=m^2-4\)
\(a)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)nghịch biến
\(\Leftrightarrow a< 0\)
\(\Leftrightarrow m^2-4< 0\)
\(\Leftrightarrow m^2< 4\)
\(\Leftrightarrow-\sqrt{4}< m< \sqrt{4}\)
\(\Leftrightarrow-2< m< 2\)
Vậy với \(-2< m< 2\)thì hàm số nghịch biến
\(b)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)đồng biến \(\forall x>0\)
\(\Leftrightarrow a>0\)
\(\Leftrightarrow m^2-4>0\)
\(\Leftrightarrow m^2>4\)
\(\Leftrightarrow\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)
Vậy với \(\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)thì hàm số đồng biến \(\forall x>0\)
BÀI 3:Xác định tham số m để hàm số y=(m^2 - 4)x-5 nghịch biến
Xác định tham số m để hàm số y=(m^2 - 1)x+2 đồng biến với mọi x>0
BÀI 6 Cho đường thẳng (d) y=-x+2 và parabol P y=1/2.x^2
a)tìm giá trị m để điểm M(m;m-1) nằm trên (d).Với m vừa tìm được chứng tỏ điểm M không thuộc P
b) vẽ P và (d) trên cùng mặt phẳng tọa độ và tìm tọa độ giao điểm của
chúng
BÀI 4:
TRONG mặt phẳng tọa độ Oxy , cho parabol P: y=-x^2
a) vẽ đồ thị P
b) gọi A và B là hai điểm thuộc P có hoành độ lần lượt là 1 , -2 .Lập phuơng trình đường thẳng AB
c) tìm phương trình đường thẳng (d) song song với đường thẳng AB và tiếp xúc với P