Cho hình vuông ABCD với O là giao điểm hai đường chéo. Tìm góc φ để phép quay Q O ; φ biến hình vuông ABCD thành chính nó.
A. φ = π 6
B. φ = π 3
C. φ = π 2
D. φ = 2 π 3
Cho hình vuông ABCD, gọi O là giao điểm của AC và BD. Tìm ảnh của các điểm A, B, O qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc 90 ° và phép đối xứng qua đường BD (h.1.41).
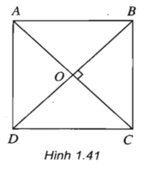
- Ảnh của A, B, O qua phép quay tâm O góc 90o lần lượt là: D, A, O
- Ảnh của D, A, O qua phép đối xứng qua đường thẳng BD là: D, C, O
Cho hình thoi ABCD, góc B tù, O là giao điểm của hai đường chéo. Kẻ BM vuông góc với AD, BN vuông góc với CD, DP vuông góc với AB, DQ vuông góc với BC. Gọi H là giao điểm của MB và PD, K là giao điểm của BN và DQ. Chứng minh: a) A, H, O thẳng hàng. b) A, H, K, C thẳng hàng. c) Tứ giác BHDK là hình thoi.
a: Xét ΔAMB vuông tại M và ΔAPD vuông tại P có
AB=AD
góc A chung
Do đó: ΔAMB=ΔAPD
=>AM=AP
Xét ΔAMH vuông tại M và ΔAPH vuông tại P có
AH chung
AM=AP
Do đó: ΔAMH=ΔAPH
=>góc MAH=góc PAH
=>AH là phân giác của góc BAD(1)
ΔABD cân tại A
mà AO là trung tuyến
nên AO là phân giác của góc BAD(2)
Từ (1), (2) suy ra A,H,O thẳng hàng
b: Xét ΔCDB có
DQ,BN là đường cao
DQ cắt BN tại K
Do đó; K là trực tâm của ΔCDB
=>CK vuông góc BD
ΔCBD cân tại C
mà CO là trung tuyến
nên CO vuông góc BD
=>C,K,O thẳng hàng
C,K,O thẳng hàng
A,H,O thẳng hàng
A,O,C thẳng hàng(ABCD là hình thoi có O là giao của hai đường chéo AC và BD)
Do đó: C,K,O,H,A thẳng hàng
=>A,H,K,C thẳng hàng
=>HK vuông góc DB
c: Xét tứ giác BHDK có
BH//DK
BK//DH
Do đó: BHDK là hình bình hành
mà HK vuông góc BD
nên BHDK là hình thoi
cho hình vuông ABCD 1 đường thẳng xy quay quanh điểm O ( O là giao điểm 2 đường chéo hình vuông ) và không đi qua đỉnh nào của hình vuông. Kẻ AA', BB',CC',DD' lần lượt vuông góc với đường thẳng xy. Cmr: AA'^2 + BB'^2 + CC'^2 + DD'^2 có độ lớn không đổi.
15. Cho hình vuông ABCD. O là giao điểm của 2 đường chéo. Hai đường thẳng m,n vuông góc với nhau tại O. Đường thẳng m cắt AB,CD lần lượt tại P,Q. Đường thẳng n cắt BC,AD lần lượt tại R,S.
a, Cm ΔAOP=ΔBOR
b, Cm OP=OR=OS=OQ
c, Cm PRSQ là hình vuông
a) Ta có thể chứng minh ΔAOP = ΔBOR bằng cách sử dụng góc vuông và góc đồng quy. Vì hai đường thẳng m và n vuông góc với nhau tại O, nên góc AOP và góc BOR là góc vuông. Đồng thời, ta cũng có góc OPA = góc ORB (do OP và OR là hai cạnh của hình vuông OPRQ). Vì vậy, theo góc đồng quy, ta có ΔAOP = ΔBOR.
b) Vì O là giao điểm của hai đường chéo của hình vuông ABCD, nên ta có OP = OR = OS = OQ.
c) Ta cũng có thể chứng minh PRSQ là hình vuông bằng cách sử dụng góc vuông và góc đồng quy. Vì hai đường thẳng m và n vuông góc với nhau tại O, nên góc PQR và góc PSR là góc vuông. Đồng thời, ta cũng có góc QPR = góc RPS (do PQ và RS là hai cạnh của hình vuông PRSQ). Vì vậy, theo góc đồng quy, ta có PRSQ là hình vuông.
Vậy, ΔAOP = ΔBOR, OP = OR = OS = OQ và PRSQ là hình vuông.
để mai mình tìm cách làm cho bạn dễ hiểu hơn
a) Vì tam giác AOB và tam giác BAQ có các góc tương đương và cạnh nhau nên chúng có cùng một hình dạng (đồng dạng). Từ đó suy ra, độ dài hai cạnh OA và OB cũng bằng nhau. b) Vì hình vuông PRSQ, các đường chéo PR, PS và RS đều chia thành các góc 90 độ. Do đó, độ dài MO bằng độ dài AS và cũng bằng độ dài BR. Ngoài ra, từ tam giác MOAS và tam giác MOBR, ta có thể thấy rằng độ dài OP bằng OR và cũng bằng OS. c) Do góc RPQ bằng góc RPS và cạnh PR bằng cạnh PS, ta suy ra hình vuông PRSQ.
Với giá trị nào của góc φ sau đây thì phép quay Q O ; φ biến hình vuông ABCD tâm O thành chính nó?
A. φ = π 2
B. φ = 3 π 4
C. φ = 2 π 3
D. φ = π 3
Với giá trị nào của góc φ sau đây thì phép quay Q O ; φ biến hình vuông ABCD tâm O thành chính nó?
A. φ = π 2
B. φ = 3 π 4
C. φ = 2 π 3
D. φ = π 3
Đáp án A
Phép quay tâm Q với góc quay φ = π 2 biến hình vuông A B C D thành chính nó
Cho hình vuông ABCD có đường chéo bằng 8cm. M là một điểm bất kì trên cạnh AB, O là giao điểm hai đường chéo. Đường thẳng qua O và vuông góc với OM cắt BC tại N. Diện tích tứ giác OMBN bằng bao nhiêu cm?
Cho hình vuông ABCD tâm O.
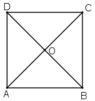
a. Tìm ảnh của điểm C qua phép quay tâm A góc 90 o .
b. Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90 o
a. Gọi C’ là điểm đối xứng với điểm C qua điểm D.
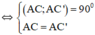 ⇔ C’ là điểm đối xứng với C qua D.
⇔ C’ là điểm đối xứng với C qua D.
b) Ta có:
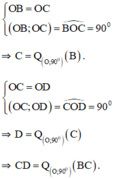
Cho hình vuông ABCD O là giao điểm hai đường chéo kẻ EF vuông góc với AD vuông góc với CD chứng minh OB = FG ;OB vuông góc với FG. các đường thẳng BO,AG,CF đồng quy.
mn giúp mình với
mình cần gấp