Tìm phép tịnh tiến T v → biến C : x + 10 2 + y − 2 2 = 16 thành C ' : x + 2 2 + y − 6 2 = 4
A.Không tồn tại v →
B. v → = − 12 ; 8
C. v → = 8 ; − 12
D. v → = 8 ; 4
Tìm phép tịnh tiến T v → biến C : x + 10 2 + y − 2 2 = 16 thành
C ' : x + 2 2 + y − 6 2 = 16
A. Không tồn tại v →
B. v → = − 12 ; 8
C. v → = 8 ; − 12
D. v → = 8 ; 4
Đáp án D
(C) có tâm I( –10 ; 2) bán kính 4, (C’) có tâm I’( –2 ; 6 ) bán kính 4
Áp dụng biểu thức tọađộ x ' = x + a y ' = y + b , ta có: a = 8 b = 4 => v → = 8 ; 4
cho 2 phép tịnh tiến T\(\overrightarrow{u}\) và T\(\overrightarrow{v}\) . Với điểm M bất kỳ , T\(\overrightarrow{u}\) biến điểm thành điểm M' , T\(\overrightarrow{v}\) biến M' thành M'' . Chứng tỏ rằng phép biến hình biến M thành M'' là một phép tịnh tiến .
M-> M' => VÊCTỚ MM'= VT u
Tv: M' -> M'' => vt M'M'' = v
áp dụng quy tắc 3 diểm => vt MM' +M'M'' = u+v =w
=> với mỗi điểm M qua phép tt theo vecto w se biến M -> M'' => ĐÓ LÀ PHÉP TT
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
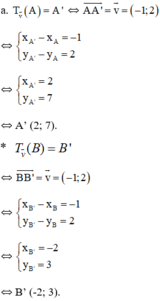
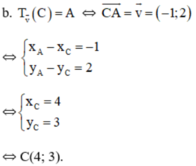
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Phép tịnh tiến theo v → = 1 ; − 2 biến điểm M(-3;1) thành điểm M'. Tìm tọa độ M'.
A. M ' 4 ; − 3
B. M'(-2;-1)
C. M'(-4;3)
D. M'(2;1)
Trong hệ trục tọa độ Oxy, cho hai đường tròn (C) và (C') lần lượt có phương trình là x - 1 2 + y + 2 2 = 4 và x + 2 2 + y - 1 2 = 4 . Xét phép tịnh tiến theo vectơ v → biến đường tròn (C) thành đường tròn (C').Tìm v → ?
A. v → = - 3 ; 3
B. v → = - 1 ; - 1
C. v → = 3 ; - 3
D. v → = 1 ; 1
Đáp án A
Ta có I ( 1 ; - 2 ) , I ' - 2 ; 1 ⇒ v → = I I ' → = - 3 ; 3 .
Trong hệ trục tọa độ Oxy, cho hai đường tròn (C), (C') lần lượt có phương trình là x - 1 2 + y + 2 2 = 4 và x + 2 2 + y - 1 2 = 4 Xét phép tịnh tiến theo vectơ v → biến đường tròn (C) thành đường tròn (C'). Tìm v →
A. v → = - 3 ; 3
B. v → = - 1 ; 1
C. v → = 3 ; - 3
D. v → = 1 ; 1
Giải giúp mình với ạ
Tìm ảnh của đường tròn ( C ): x2 + y2 - 2x - 4 = 0 qua liên tiếp các phép biến hình sau:
phép vị tự V( O; -2 ), phép tịnh tiến T\(\overrightarrow{v}\) ( 1; -2 )
Trong mặt phẳng Oxy cho đường tròn (C): x 2 + y 2 + 2 x − 4 y – 11 = 0 . Tìm phép tịnh tiến biến (C) thành (C′): x − 10 2 + y + 5 2 = 16
(C) có tâm I(−1;2), bán kính R = 4. (C’) có tâm I′(10; −5), bán kính R’ = 4. Vậy ( C ′ ) = T v → ( C ) , v → = I I ' → = ( 11 ; − 7 ) .
cho a(3;0), b(-2;4), c(-4;5) phép tịnh tiến theo vecto v(1;4) biến tam giác abc thành tam giác a'b'c' tìm tọa độ trọng tâm tam giác abc
Gọi G là trọng tâm ABC \(\Rightarrow G\left(-1;3\right)\)
\(T_{\overrightarrow{v}}\left(G\right)=G'\Rightarrow\left\{{}\begin{matrix}x'=-1+1=0\\y'=3+4=7\end{matrix}\right.\)
\(\Rightarrow G'\left(0;7\right)\)