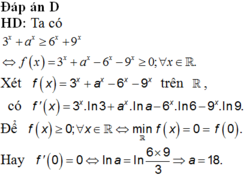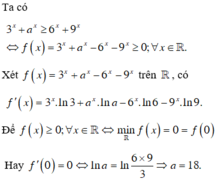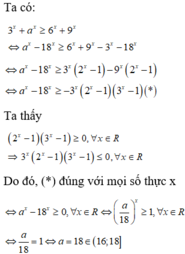Chứng minh đẳng thức, bất đẳng thức: \(9x^2-6x+2>0\) với mọi x
DD
Những câu hỏi liên quan
Chứng minh đẳng thức, bất đẳng thức: \(x^2+x+1>0\) với mọi x
Lời giải:
$x^2+x+1=x^2+2.x.\frac{1}{2}+(\frac{1}{2})^2+\frac{3}{4}$
$=(x+\frac{1}{2})^2+\frac{3}{4}$
$\geq 0+\frac{3}{4}$
$> 0$
Ta có đpcm.
Chứng minh đẳng thức, bất đẳng thức: \(2x^2+2x+1>0\) với mọi x
Ta có: \(2x^2+2x+1\)
\(=2\left(x^2+x+\frac{1}{2}\right)\)
\(=2\left(x^2+2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{1}{4}\right)\)
\(=2\left(x+\frac{1}{2}\right)^2+\frac{1}{2}\)
Ta có: \(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\forall x\)
hay \(2x^2+2x+1>0\forall x\)(đpcm)
Đúng 0
Bình luận (0)
Chứng minh đẳng thức, bất đẳng thức: \(2x^2+2x+1>0\) với mọi x
Chứng minh đẳng thức, bất đẳng thức: \(2x^2+2x+1\)>0 với mọi x
https://i.imgur.com/QBCcqpP.jpg
Biết rằng a là số thực dương sao cho bất đẳng thức
3
x
+
a
x
⩾
6
x
+
9
x
đúng với mọi số thực x. Mệnh đề nào sau đây đúng?
Đọc tiếp
Biết rằng a là số thực dương sao cho bất đẳng thức 3 x + a x ⩾ 6 x + 9 x đúng với mọi số thực x. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Biết rằng a là số thực dương sao cho bất đẳng thức
3
x
+
a
x
≥
6
x
+
9
x
đúng với mọi số thực x. Mệnh đề nào sau đây đúng? A.
a
∈
12
;
14
B.
a
∈...
Đọc tiếp
Biết rằng a là số thực dương sao cho bất đẳng thức 3 x + a x ≥ 6 x + 9 x đúng với mọi số thực x. Mệnh đề nào sau đây đúng?
A. a ∈ 12 ; 14
B. a ∈ 10 ; 12
C. a ∈ 14 ; 16
D. a ∈ 16 ; 18
Biết rằng a là số thực dương sao cho bất đẳng thức
3
x
+
a
x
≥
6
x
+
9
x
đúng với mọi số thực x. Mệnh đề nào sau đây đúng? A.
a
∈
( 12; 14] B.
a
∈
( 10;12] C.
a
∈
( 14;16] D.
a
∈
(16;18]
Đọc tiếp
Biết rằng a là số thực dương sao cho bất đẳng thức 3 x + a x ≥ 6 x + 9 x đúng với mọi số thực x. Mệnh đề nào sau đây đúng?
A. a ∈ ( 12; 14]
B. a ∈ ( 10;12]
C. a ∈ ( 14;16]
D. a ∈ (16;18]
chứng minh bất đẳng thức:|3x-2y| ≤ 2 với 9x² +4x²=1.dấu = xảy ra khi nào?
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b) 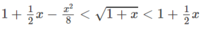
với 0 < x < + ∞
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
![]()
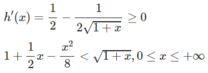
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
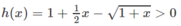
Hay
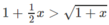
Xét hàm số trên f(x) trên [0; + ∞ );
![]()
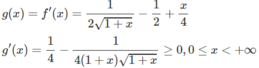
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
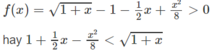
Với mọi 0 < x < + ∞ .
Đúng 0
Bình luận (0)