Bài 1: Tìm x
x^n(x+1)-x^n-x^n-1=0
Bài 2 Tìm a
12x^2+24x-15=(2x-a)(6x-3)
Bài 1: Tìm x
x^n(x+1)-x^n-x^n-1=0
Bài 2 Tìm a
12x^2+24x-15=(2x-a)(6x-3)
Bài 1. Đề khó nhìn quá mình không làm được ._.
Bài 2.
12x2 + 24x - 15 = ( 2x - a )( 6x - 3 )
<=> 12x2 + 24x - 15 = 12x2 - 6x - 6ax + 3a
<=> 12x2 + 24x - 15 = 12x2 + ( -6 - 6a )x + 3a
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}-6-6a=24\\-15=3a\end{cases}}\Leftrightarrow a=-5\)
Bài 1.Tìm số nguyên n sao cho n+6 chia hết cho n+2
Bài 2. Tìm số nguyên n sao cho 3n+2 chia hết cho n+1
Bài 3. Tìm số nguyên x biết (x-2).(x+3)<0
Bài 4. Tìm số nguyên x biết (4-2x).(x+3)>0
Bài 5.5: Tìm x: (2x-3)(x+1)+(4x\(^3\)-6x\(^2\)-6x):(-2x)=18
Bài 6.1: Tìm số tự nhiên n để: 5x\(^{n-2}\):3x\(^2\)
Bài 6.2: Tìm số tự nhiên n để đa thức x\(^{n-1}\)-3x\(^2\):2x\(^2\)
Bài 6.3: Tìm n ∈ N để phép tính chia sau là phép chia hết:
3x\(^7\)y\(^7\)-4x\(^6\)y\(^6\)-5x\(^3\)y\(^3\):(2x\(^n\)y\(^n\))
Trả lời nhanh giúp mìn nhóe!![]()
Bài 5.5:
\(\left(2x-3\right)\left(x+1\right)+\left(4x^3-6x^2-6x\right):\left(-2x\right)=18\)
\(\Leftrightarrow\left(2x^2+2x-3x-3\right)+2x\cdot\left(2x^2-3x-3\right):\left(-2x\right)=18\)
\(\Leftrightarrow2x^2-x-3-2x^2+3x+3=18\)
\(\Leftrightarrow2x=18\)
\(\Leftrightarrow x=\dfrac{18}{2}\)
\(\Leftrightarrow x=9\)
Bài 1 : Tìm x biết :
xn (x + 1) - xn - xn-1 = 0
Bài 2 : Tìm a biết :
12x2 + 24x - 15 = (2x - a)(6x - 3)
B1:
\(x^n\left(x+1\right)-x^n-x^{n-1}=0\)
\(\Rightarrow x^{n-1}\left(x^2+x\right)-x^{n-1}.x-x^{n-1}=0\)
\(\Rightarrow x^{n-1}\left(x^2+x-x-1\right)=0\)
\(\Rightarrow x^{n-1}\left(x^2-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x^{n-1}=0\\x^2-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Bài 1: Tìm x; biết:
a) 2x^2-8x=0 b) (x+2)^2-x(x-1)=10 c)b x^3-6x^2+9x=0
Bài 2: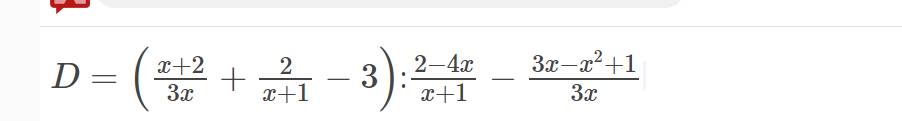
a) Viết điều kiện xác định của biểu thức D
b) Rút gọn biểu thức D
c) Tính giá trị của D khi x=1/
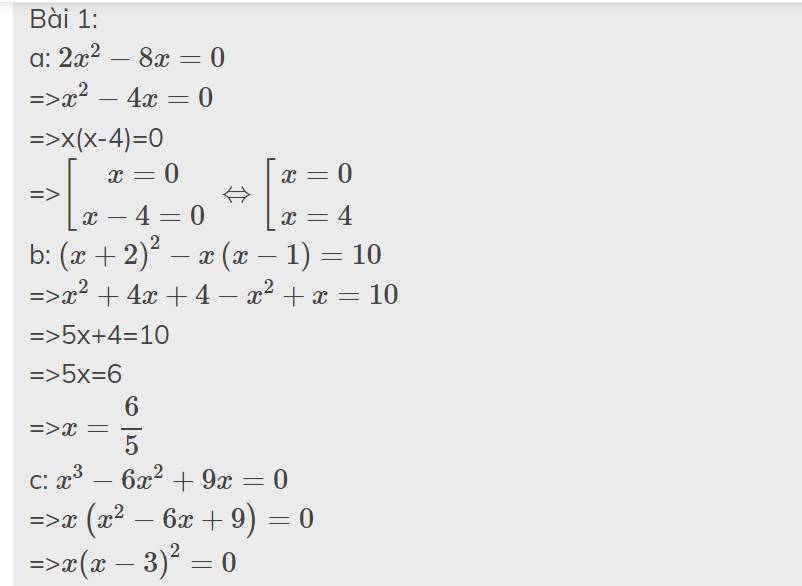
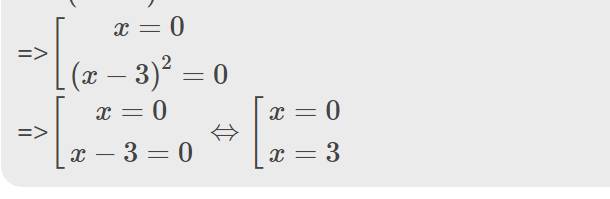 Bài 2:
Bài 2:
a: ĐKXĐ: \(x\notin\left\{0;-1;\dfrac{1}{2}\right\}\)
b: \(D=\left(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\right):\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
\(=\dfrac{\left(x+2\right)\left(x+1\right)+6x-3\cdot3x\left(x+1\right)}{3x\left(x+1\right)}\cdot\dfrac{x+1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{x^2+3x+2+6x-9x^2-9x}{3x}\cdot\dfrac{1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-8x^2+2}{3x}\cdot\dfrac{1}{-4x+2}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-2\left(2x-1\right)\left(2x+1\right)}{3x\cdot\left(-2\right)\left(2x-1\right)}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1}{3x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1+x^2-3x-1}{3x}=\dfrac{x^2-x}{3x}=\dfrac{x-1}{3}\)
c: Khi x=1 thì \(D=\dfrac{1-1}{3}=0\)
bài 1 ; 6x(x+2018)-3(x+2018)=0
bài 2; x(x-11)+3(11-x)=0
bài 3; x(x-3)-2(3-x)=0
bài 4; 2x(x+5)-4(x+5)=0
mấy bạn giúp mình với ạ
1: =>(x+2018)(6x-3)=0
=>x+2018=0 hoặc 6x-3=0
=>x=1/2 hoặc x=-2018
2: x(x-11)+3(11-x)=0
=>(x-11)(x-3)=0
=>x=11 hoặc x=3
4: =>(x+5)(2x-4)=0
=>2x-4=0 hoặc x+5=0
=>x=2 hoặc x=-5
3: =>(x-3)(x+2)=0
=>x=3 hoặc x=-2
Bài 1:
\(6x\left(x+2018\right)-3\left(x+2018\right)=0\)
\(\Leftrightarrow\left(x+2018\right)\left(6x-3\right)=0\)
\(\Leftrightarrow3\left(x+2018\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2018\\2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2018\\x=\dfrac{1}{2}\end{matrix}\right.\)
Bài 2:
\(x\left(x-11\right)+3\left(11-x\right)=0\)
\(\Leftrightarrow x\left(x-11\right)-3\left(x-11\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-11\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=11\end{matrix}\right.\)
Câu 3:
\(x\left(x-3\right)-2\left(3-x\right)=0\)
\(\Leftrightarrow x\left(x-3\right)+2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Câu 4:
\(2x\left(x+5\right)-4\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\2x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
Tìm GTLN - GTNN của các biểu thức ?
* bài 1: Tìm GTNN:
a) A= (x - 5)² + (x² - 10x)² - 24
b) B= (x - 7)² + (x + 5)² - 3
c) C= 5x² - 6x +1
d) D= 16x^4 + 8x² - 9
e) A= (x + 1)(x - 2)(x - 3)(x - 6)
f) B= (x - 2)(x - 4)(x² - 6x + 6)
g) C= x^4 - 8x³ + 24x² - 8x + 25
h) D= x^4 + 2x³ + 2x² + 2x - 2
i) A= x² + 4xy + 4y² - 6x – 12y +4
k) B= 10x² + 6xy + 9y² - 12x +15
l) C= 5x² - 4xy + 2y² - 8x – 16y +83
m) A= (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9
* Bài 2: Tìm GTLN:
a) M= -7x² + 4x -12
b) N= -16x² - 3x +14
c) M= -x^4 + 4x³ - 7x² + 12x -5
d) N= -(x² + x – 2) (x² +9x+18) +27
* Bài 3:
1) Cho x - 3y = 1. Tìm GTNN của M= x² + 4y²
2) Cho 4x - y = 5. Tìm GTNN của 3x²+2y²
3) Cho a + 2b = 2. Tìm GTNN của a³ + 8b³
* Bài 4: Tìm GTLN và GTNN của các biểu thức:
1) A = (3 - 4x)/(x² + 1)
2) B= (8x + 3)/(4x² + 1)
3) C= (2x+1)/(x²+2)
Bài 1: Tìm x; biết:
a) 2x^2-8x=0 b) (x+2)^2-x(x-1)=10 c)b x^3-6x^2+9x=0
Bài 2:
a) Viết điều kiện xác định của biểu thức D
b) Rút gọn biểu thức D
c) Tính giá trị của D khi x=1/2
Bài 1:
a: \(2x^2-8x=0\)
=>\(x^2-4x=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b: \(\left(x+2\right)^2-x\left(x-1\right)=10\)
=>\(x^2+4x+4-x^2+x=10\)
=>5x+4=10
=>5x=6
=>\(x=\dfrac{6}{5}\)
c: \(x^3-6x^2+9x=0\)
=>\(x\left(x^2-6x+9\right)=0\)
=>\(x\left(x-3\right)^2=0\)
=>\(\left[{}\begin{matrix}x=0\\\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Bài 1 Tìm x, biết
a, (x+1).(x+2)-(x-1).(x-5)=0
b, (2x-1)^2+4x(5-x)=15
Bài 2 Tìm giá trị nhỏ nhất của
a, M=x^2-6x+6
b,N=4x^2+x-2
Bài 1:
a; (\(x+1\)).(\(x+2\)) - (\(x-1\)).(\(x-5\)) = 0
\(x^2\) + 2\(x\) + \(x+2\) - \(x^2\) + 5\(x\) + \(x\) - 5 = 0
(\(x^2\) - \(x^2\)) + (2\(x\) + \(x+5x+x\))- (5 -2) = 0
0 + (3\(x\) + 5\(x\) + \(x\)) + 0 - 3 = 0
8\(x\) + \(x\) - 3 = 0
9\(x\) = 3
\(x=\dfrac{3}{9}\)
Vậy \(x=\dfrac{1}{3}\)
b; (2\(x\) - 1)2 + 4.(5 - \(x\)) = 15
4\(x^2\) - 4\(x\) + 1 + 20 - 4\(x\) = 15
4\(x^2\) - (4\(x\) + 4\(x\)) + (1 + 20 - 15) = 0
4\(x^2\) - 8\(x\) + 6 = 0
4.(\(x^2\) - 2\(x\) + 1) + 2 = 0
4(\(x-1\))2 + 2 = 0
Vì 4.(\(x-1\))2 ≥ 0 ⇒ 4.(\(x-1\))2 + 2 ≥ 3 > 0 (\(\forall x\))
Vậy không có giá trị nào của \(x\) thỏa mãn đề bài
Kết luận \(x\) \(\in\) \(\varnothing\)
Bài 2:
a; M = \(x^2\) - 6\(x\) + 6
M = (\(x^2\) - 2.3\(x\) + 32) - 3
M = (\(x\) - 3)2 - 3 vì (\(x-3\))2 ≥ 0 ∀ \(x\); ⇒ (\(x-3\))2 - 3 ≥ -3
Vậy Mmin = - 3 khi \(x-3\) = 0 ⇒ \(x=3\)
Vậy Giá trị nhỏ nhất của biểu thức là -3 khi \(x=3\)