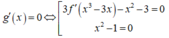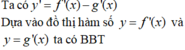Cho y=g(x+1)=3x-2. Tìm hàm số y=g(x)
PH
Những câu hỏi liên quan
Cho hàm số y=g(x)=3x-2. Tính g(0), g(-1), g(-2)
Cho hàm số y = g(x) = |3x-1|
a) Tính g(-2) ; \(g\left(-\frac{1}{4}\right)\)
b) Viết cặp giá trị (x , y)
biết \(x\in\left\{-2;-1;0;1;2\right\}\)
c) Tìm x sao cho g(x) = 10 ; g(x) = -3
d) x có là hàm số của g không? Vì sao?
Cho hàm số y= F(x) = x×(x-2) và hàm số y= G(x) = -x+6
a) tính F(3); [ F(2/3) ]² ; G(-1/2)
b) tìm x để F(x)=0
c) tìm a để F(a)=G(a)
a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)
\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)
\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)
\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)
b: F(x)=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
c: F(a)=G(a)
=>\(a\left(a-2\right)=-a+6\)
=>\(a^2-2a+a-6=0\)
=>\(a^2-a-6=0\)
=>(a-3)(a+2)=0
=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
1.Cho hàm số y = g(x) = x - 4. Khi đó g(-2) bằng
A.-2 B.2 C.-6 D.6
2.Cho hàm số y = f(x) = -3x+ 5. Nếu f(x) = -7 thì x bằng
A.2/3 B.-4 C.2 D.4
Cho hàm số y f( x) có đạo hàm
f
(
x
)
x
2
(
x
-
9
)
(
x
-
4
)
2
.
Xét hàm số y g( x) f( x2) Trong các phát biểu sau; tìm số phát biểu đúng I. Hàm số y g( x) đồng biến trên( 3; +∞) II. Hàm số y g(x) nghịch biến trê...
Đọc tiếp
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV. m i n x ∈ R g ( x ) = f ( 9 )
A. 1
B. 2
C. 3
D. 4
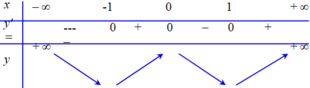
Ta có
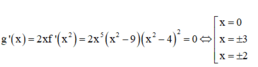
Bảng biến thiên của hàm số y= g( x)
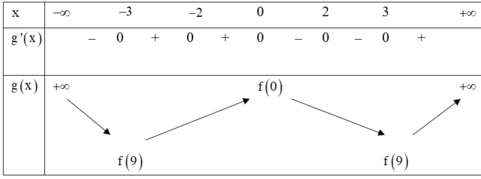
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.
Đúng 0
Bình luận (0)
cho hàm số y = f(x) liên tục trên R sao cho \(\max\limits_{\left[-8;\dfrac{8}{3}\right]}=5\). xét hàm số \(g\left(x\right)=2f\left(\dfrac{1}{3}x^3-x^2-3x+1\right)+m\). tìm tất cả các giá trị thực của tham số m để \(\max\limits_{\left[-2;4\right]}g\left(x\right)=-20\)
Dựa vào đồ thị của hai hàm số đã cho trong hình 14
y = f(x) = x + 1 và y = g(x) = 1/2 x2
Hãy:
a) Tính f(-2), f(-1), f(0), f(2), g(-1), g(-2), g(0);
b) Tìm x, sao cho f(x) = 2;
Tìm x, sao cho g(x) = 2;
a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3
g(-1) = 0,5; g(-2) = 2; g(0) = 0
b) f(x) = 2 ⇒ x = 1
g(x) = 2 ⇒ x = 2 hoặc x = -2
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có bảng biến thiên như sau Tìm giá trị lớn nhất của hàm số g(x)
f
x
3
-
3
x
-
1
5
x
5
-
2
3
x
3
+
3
x
-
2
15
trên đoạn [...
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như sau
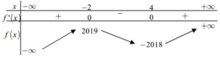
Tìm giá trị lớn nhất của hàm số g(x) = f x 3 - 3 x - 1 5 x 5 - 2 3 x 3 + 3 x - 2 15 trên đoạn [-1;2]?
A. 2022
B. 2019
C. 2020
D. 2021
Cho hai hàm số y f(x) và y g(x) có đồ thị của hàm y f (x), y g(x) như hình vẽ. Tìm các khoảng đồng biến của hàm số y f(x) - g(x) A.
-
1
;
0
;
1
;
+
∞
B.
-
∞
;
-
1...
Đọc tiếp
Cho hai hàm số y = f(x) và y = g(x) có đồ thị của hàm y = f '(x), y = g'(x) như hình vẽ. Tìm các khoảng đồng biến của hàm số y = f(x) - g(x)
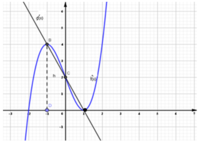
A. - 1 ; 0 ; 1 ; + ∞
B. - ∞ ; - 1 ; 0 ; 1
C. 1 ; + ∞ ; - 2 ; - 1
D. - 2 ; + ∞