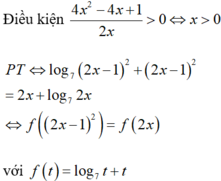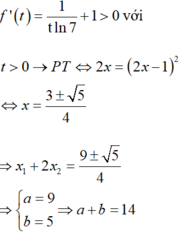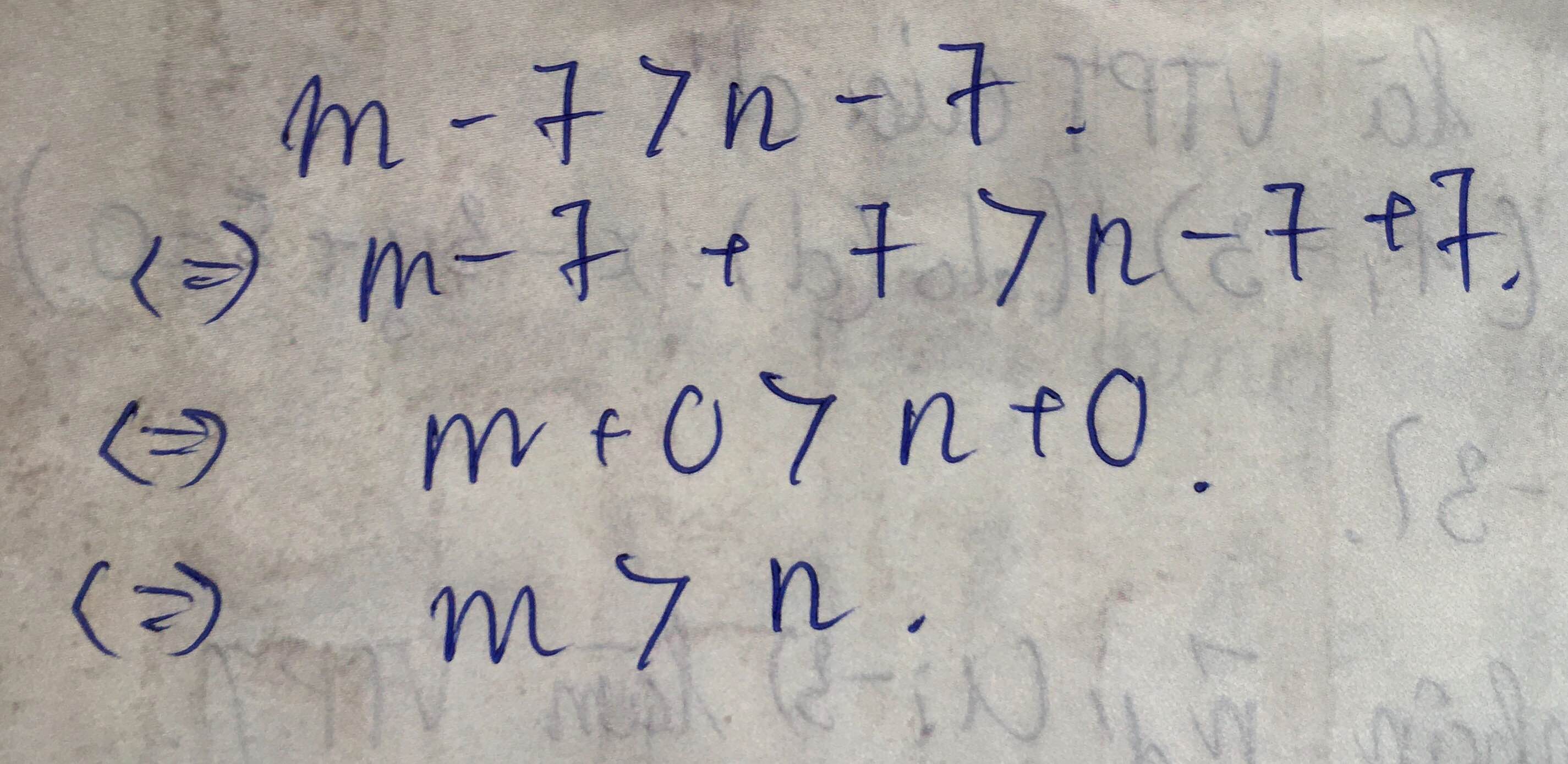Bài 3: Tìm hai số a,b biết \(14a=12b\) và \(a+b=130\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PN
Những câu hỏi liên quan
Tìm hai số nguyên a và b biết 27a = 12b; a và b có ước chung lớn nhất là 2015
Tìm hai số tự nhiên a, b (a>b), biết a + b = 30 và BCNN(a, b) = 6. ƯCLN (a, b).
a = 10 ; b = 20
a = 12 ; b = 18
a = 16 ; b = 14
a = 18 ; b = 12
Câu 4 Mã: 74288
Tìm các số tự nhiên a và b (a < b) biết ab = 48 và ƯCLN (a, b) = 4.
a = 1, b = 48
a = 2, b = 24
a = 3, b = 16
a = 4, b = 12
1. Cho a ,b là các số nguyên thỏa mãn :
( 14a - 7b + 4 )( 4a + 2b + 1 ) \(⋮\)7
Chứng minh rằng : ( 25a - 12b + 8 ) \(⋮\)7
2. Tìm các số nguyên x, y biết :
x - 3 = y( x+ 2 )
2. Ta có: x - 3 = y(x - 2)
=> x - 3 - y(x - 2) = 0
=> (x - 2) - y(x - 2) = 1
=> (1 - y)(x - 2) = 1
=> 1 - y; x - 2 \(\in\)Ư(1) = {1; -1}
Lập bảng :
| 1 - y | 1 | -1 |
| x - 2 | 1 | -1 |
| y | 0 | 2 |
| x | 3 | 1 |
Vậy ...
Đúng 0
Bình luận (0)
Biết
x
1
,
x
2
là hai nghiệm của phương trình
log
7
4
x
2
−
4
x
+
1
2
x
+
4...
Đọc tiếp
Biết x 1 , x 2 là hai nghiệm của phương trình log 7 4 x 2 − 4 x + 1 2 x + 4 x 2 + 1 = 6 x và x 1 + 2 x 2 = 1 4 a + b với a, b là hai số nguyên dương. Tính a + b
A. a + b = 16
B. a + b = 14
C. a + b = 13
D. a + b = 11
Chọn B.
Phương pháp:
Giải phương trình bằng phương pháp xét hàm số.
Cách giải:


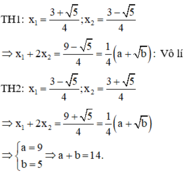
Đúng 0
Bình luận (0)
Bài 2. Tìm tất cả các số nguyên tố a, b, c thỏa mãn a+b+c+6 là một số chính phương không chia hết cho 3 và ab+bc+ca+12a+12b+12c−30 là một số chính phương.
Cho a,b là các số nguyên thỏa mãn
(14a - 7b + 4)(4a +2b + 1) chia hết cho 7
Chứng minh rằng: (25a -12b +8 ) chia hết cho 7
\(14a-7b+4=7\left(2a-b+1\right)-3⋮7̸\)\(\Rightarrow4a+2b+1⋮7\Leftrightarrow4a+21a+2b-14b+1+7⋮7\Leftrightarrow25a-12b+8⋮7\)
Đúng 0
Bình luận (0)
\(14a-7b+4=7\times\left(2a-b\right)+4⋮̸7\)
\(\left(14a-7b+4\right)\left(4a+2b+1\right)⋮7\)
\(\Rightarrow4a+2b+1⋮7\)
\(21a-14b+7⋮7\)
\(\Rightarrow\left(4a+2b+1\right)+\left(21a-14b+7\right)⋮7\)
\(\Rightarrow\left(4a+21a\right)-\left(14b-2b\right)+\left(1+7\right)⋮7\)
\(\Rightarrow25a-12b+8⋮7\)
Đúng 0
Bình luận (0)
Biết
x
1
,
x
2
là hai nghiệm của phương trình
log
7
4
x
2
−
4
x
+
1
2
x
+
4
x...
Đọc tiếp
Biết x 1 , x 2 là hai nghiệm của phương trình log 7 4 x 2 − 4 x + 1 2 x + 4 x 2 + 1 = 6 x và x 1 , x 2 thỏa mãn x 1 + 2 x 2 = 1 4 a + b với a, b là hai số nguyên dương. Tính a + b .
A. a + b = 16
B. a + b = 11
C. a + b = 14
D. a + b = 13
Đáp án C
Điều kiện 4 x 2 − 4 x + 1 2 x > 0 ⇔ x > 0
P T ⇔ log 7 2 x − 1 2 + 2 x − 1 2 = 2 x + log 7 2 x ⇔ f 2 x − 1 2 = f 2 x
với f t = log 7 t + t
f ' t = 1 t ln 7 + 1 > 0 với t >0
→ P T ⇔ 2 x = 2 x − 1 2 ⇔ x = 3 ± 5 4
⇒ x 1 + 2 x 2 = 9 ± 5 4 ⇒ a = 9 b = 5 ⇒ a + b = 14
Đúng 0
Bình luận (0)
Biết x1, x2 là hai nghiệm của phương trình
log
7
4
x
2
-
4
x
+
1
2
x
+
4
x
2
+
1
6
x
và x1, x2 t...
Đọc tiếp
Biết x1, x2 là hai nghiệm của phương trình log 7 4 x 2 - 4 x + 1 2 x + 4 x 2 + 1 = 6 x và x1, x2 thỏa mãn x 1 + 2 x 2 = 1 4 a + b với a, b là hai số nguyên dương. Tính a + b.
A. a + b = 16
B. a + b = 11
C. a + b = 14
D. a + b = 13
Bài 1:Cho m3b b) -12b>8b c) -6b lớn hơn hoặc bằng 9b Bài 3: so sánh m và n biết a)m-7 > n-7 b) 3m