cho a(x)=5x4-3x2-2x3+4-5x4+5x2-x+2x3+1
thu gọn a(x) rồi tìm bậc a(x)
ND
Những câu hỏi liên quan
Cho
p
(
x
)
5
x
4
+
4
x
3
-
3
x
2
+
2
x
-
1
và
q
(
x
)
-
x
4...
Đọc tiếp
Cho p ( x ) = 5 x 4 + 4 x 3 - 3 x 2 + 2 x - 1 và q ( x ) = - x 4 + 2 x 3 - 3 x 2 + 4 x - 5
Tính p(x) + q(x) rồi tìm bậc của đa thức thu được
A. p ( x ) + q ( x ) = 6 x 3 - 6 x 2 + 6 x - 6 có bậc là 6
B p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x + 6 có bậc là 4
C. p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 có bậc là 4
D. P ( x ) + q ( x ) = 4 x 4 + 6 x 3 + 6 x - 6 c ó b ậ c l à 4
Ta có p(x) + q(x)
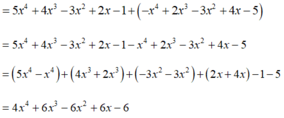
Bậc của đa thức p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 l à 4
Chọn đáp án C
Đúng 0
Bình luận (0)
a)(-3x2+5x2-9x+15):(-3x+5)
b)(x4-2x3+2x-1):(x2-1)
c)(5x4+9x3-2x2-4x-8):(x-1)
d)(5x3+14x2+12x+8):(x+2)
b: \(\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}\)
\(=x^2-2x+1\)
\(=\left(x-1\right)^2\)
c: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=5x^3+14x^2+12x+8\)
Đúng 1
Bình luận (0)
cho hai đa thức:
A(x) = x5 – 3x2 + 7x4 – 9x3 + x2 – ¼ x
B(x) = 5x4 – x5 + x2 – 2x3 +3x2 – ¼
a, thu gọn và sắp xếp đa thức trên lũy thừ giảm dần của 1 biến
b, tính f(x) + A(x) + B(x); g(x) = A(x) – B(x)
c, tính giá trị của đa thức g(x) tại x = -1
b)
Sửa đề: f(x)=A(x)+B(x)
Ta có: f(x)=A(x)+B(x)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
a) Ta có: \(A\left(x\right)=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3+\left(-3x^2+x^2\right)-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Ta có: \(B\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+\left(x^2+3x^2\right)-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
b) Ta có: G(x)=A(x)-B(x)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x+x^5-5x^4+2x^3-4x^2+\dfrac{1}{4}\)
\(=2x^5+2x^4-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
A(x) = 5x2 – 2x3 + 4x5 + 3x3 – 3x2 + 2x – 1 B(x) = – x 5 + 2x3 – 3x5 – 2x2 – 3x3 + 3x – 5
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến. Chỉ ra bậc của mỗi đa thức.
b) Tính C(x) = A(x) + B(x). c) Tính C( – 1). d) Tìm nghiệm của đa thức C(x).
Thu gọn các đa thức sau rồi sắp xếp các hạng tử của chúng theo lũy thừa giảm dần của biến, tìm bậc, hệ số cao nhất, hệ số tự do:P(x)33 + x2 + 4x4 - x- 3x3 + 5x4 + x2 - 6Q(x)2x3 - x4 - dfrac{1}{2}x2 - 3 + dfrac{3}{4}x- dfrac{1}{3}x2 + x4 - dfrac{7}{4}x
Đọc tiếp
Thu gọn các đa thức sau rồi sắp xếp các hạng tử của chúng theo lũy thừa giảm dần của biến, tìm bậc, hệ số cao nhất, hệ số tự do:
P(x)=33 + x2 + 4x4 - x- 3x3 + 5x4 + x2 - 6
Q(x)=2x3 - x4 - \(\dfrac{1}{2}\)x2 - 3 + \(\dfrac{3}{4}\)x- \(\dfrac{1}{3}\)x2 + x4 - \(\dfrac{7}{4}\)x
Sửa đề: \(P=3x^3+x^2+4x^4-x-3x^3+5x^4+x^2-6\)
Ta có: \(P=3x^3+x^2+4x^4-x-3x^3+5x^4+x^2-6\)
\(=9x^4+2x^2-x-6\)
Ta có: \(Q\left(x\right)=2x^3-x^4-\dfrac{1}{2}x^2-3+\dfrac{3}{4}x-\dfrac{1}{3}x^2+x^4-\dfrac{7}{4}x\)
\(=2x^3-\dfrac{5}{6}x^2-x-3\)
Đúng 1
Bình luận (0)
Cho hai đa thức:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
Tính f(x) + g(x) và f(x) – g(x)
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
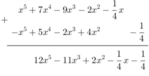
* f(x) - g(x)
Đúng 0
Bình luận (0)
Tìm hệ số tự do của hiệu f(x) - 2.g(x) với
f
(
x
)
5
x
4
+
4
x
3
-
3
x
2
+
2
x
-
1
;
g
(
x
)
...
Đọc tiếp
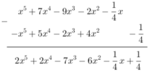
Tìm hệ số tự do của hiệu f(x) - 2.g(x) với
f ( x ) = 5 x 4 + 4 x 3 - 3 x 2 + 2 x - 1 ; g ( x ) = - x 4 + 2 x 3 - 3 x 2 + 4 x + 5
A. 7
B. 11
C. -11
D. 4
- Ta có:
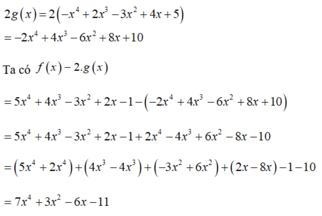
Hệ số cần tìm là -11
Chọn đáp án C
Đúng 0
Bình luận (0)
Tìm hệ số tự do của hiệu f(x) - 2.g(x) với
f
(
x
)
5
x
4
+
4
x
3
-
3
x
2
+
2
x
-
1
;
g
(
x
)
-
x
4
+
2
x...
Đọc tiếp
Tìm hệ số tự do của hiệu f(x) - 2.g(x) với
f ( x ) = 5 x 4 + 4 x 3 - 3 x 2 + 2 x - 1 ; g ( x ) = - x 4 + 2 x 3 - 3 x 2 + 4 x + 5
A. 7
B. 11
C. -11
D. 4
+) Ta có
2 g ( x ) = 2 − x 4 + 2 x 3 − 3 x 2 + 4 x + 5 = − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 Ta có f ( x ) − 2 ⋅ g ( x ) = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 − − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 + 2 x 4 − 4 x 3 + 6 x 2 − 8 x − 10 = 5 x 4 + 2 x 4 + 4 x 3 − 4 x 3 + − 3 x 2 + 6 x 2 + ( 2 x − 8 x ) − 1 − 1 = 7 x 4 + 3 x 2 − 6 x − 11
Hệ số cần tìm là -11
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho các đa thức : P(x) = x5 - 3x2 + 7x4 - 9x3 + x2 - \(\dfrac{1}{4}\)x ; Q(x) = 5x4 - x5 + x2 - 2x3 + 3x2 - \(\dfrac{1}{4}\)
a ) sắp xếp hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến
b ) Tính P(x) + Q(x)