1. chứng tỏ rằng : (a^n)^m= am.n (a,m ∈ N ; n ∈ N*)
2. so sánh : 5333 và 3555 , 2400 và 4200
3. chứng tỏ : 32008 là số có ít hơn 1005 chữ số
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Với số thực a và các số nguyên m, n, ta có:
am.an=am.n;aman=am−nam.an=am.n;aman=am−n
b) Với hai số thực a, b cùng khác 0 và số nguyên n, ta có:
(ab)n=an.bn;(ab)n=anbn(ab)n=an.bn;(ab)n=anbn
c) Với hai số thực a, b thỏa mãn 0 < a < b với số nguyên a, ta có an < bn
d) Với số thực a khác 0 và hai số nguyên m, n, ta có: Nếu m>n thì am>an
(am là a mũ m,an là amux n nha giúp mik )
cho phân số a/b ( a,b thuộc N , b khác 0 )
1. Nếu a/b < 1 và m thuộc N , m khác 0 . Chứng tỏ rằng :
a/b < a+m/b+m
2. Nếu a/b > 1 và m thuộc N , m khác 0 . Chứng tỏ rằng :
a/b > a+m/b+m
1. Do \(\frac{a}{b}< 1\Leftrightarrow\)a<b \(\Leftrightarrow\)a+n<b+n
Ta có: \(\frac{a}{b}\)= 1 - \(\frac{a-b}{b}\)
\(\frac{a+n}{b+n}\)= 1- \(\frac{a-b}{b+n}\)
Do \(\frac{a-b}{b}\)>\(\frac{a-b}{b+n}\)=> \(\frac{a}{b}\)<\(\frac{a+n}{b+n}\)
2.Tương tự
a) Chứng tỏ rằng (a m)n = với a , m ϵ N, n ϵ N*
b) So sánh 5333 và 3 555 ; 2400 và 4400
c) Chứng tỏ rằng 32008 là số có ít hơn 1005 chữ số.
b)Ta có:5333=(53)111=125111<243111=(35)111=3555
Ta có:2400<2800=4400
b) 5333 và 3555
5333=(53)111=125111
3555=(35)111=243111
Vì 125111<243111 nên 5333<3555
2400 và 4400
Vì 2<4 nên 2400<4400
Có ai biết làm cả ko giúp mình với ạ![]()
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: 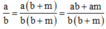
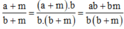
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó 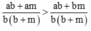
Hay 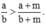
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
Chứng tỏ rằng
a, Chứng tỏ rằng trong 5 số tự nhiên liên tiếp có một số chia hết cho 3
b, Chứng tỏ rằng (9m+1) (9m+2) (9m+3) (9m+4) chia hết cho 5 với mọi n thuộc N
a, Gói 5 số tự nhiên liên tiếp là a,á+1,a+2.a+3.a+4(a thuộc N)
+Nếu a chia hết cho 5 , bài toán giải xong
+ Nếu a chia 5 dư 1, đặt a=5b+1(b thuộc N ) ta có a+4=5b+1+4=(5b+5) chia hết cho 5
+ Nếu a chia 5 dư 2, đặt a=5c+2 (c thuộc N) ta có a+3=5c+2+3=(5c+5) chia hết cho 5
+ Nếu a chia 5 dư 3 , đặt a=5d+3(d thuộc N) ta có a+2=5đ +3+2=(5d+5) chia hết cho5
+ Nếu a chia 5 dư 3, đặt a= 5e +4 ( e thuốc N ) ta có a+1=5e+4+1=(5e+5) chia hết cho 5
Vậy trong 5 số tự nhiên liên tiếp, có một số chia hết cho 5
b, 19 m+19m+1,19m+2,19m+3,19m+4 là 5 số tự nhiên liên tiếp nên theo câu a có 1 số chia hết cho 5 ma 19m ko chia hết cho 5 với mọi m thuộc N
do đó : 19m+1,19m+2,19m+3,19m+4 có 1 số chia hết cho 5
=>(19m+1);(19m+2) (19m+3), (19m+4) chia hết cho 5
cho phân số a/b(a, b thuộc N). Giả sử a/b <1 và m thuộc N, m khác ). Chứng tỏ rằng a/b<a+m/b+m
bạn giúp mình mình sẽ giúp bạn nhé
ta có : x < y hay a/m < b/m => a < b.
So sánh x, y, z ta chuyển chúng cùng mẫu : 2m
x = a/m = 2a/ 2m và y = b/m = 2b/2m và z = (a + b) / 2m
mà : a < b
suy ra : a + a < b + a
hay 2a < a + b
suy ra x < z (1)
mà : a < b
suy ra : a + b < b + b
hay a + b < 2b
suy ra z < y (2)
:D
Hãy chứng tỏ rằng nếu a chia hết cho m, a chia hết cho n mà (m,n)=1 thì a chia hết cho m.n
Chứng tỏ rằng
a) (m+1)^2>=4m
b) m^2+n^2+2>=2×(m+n)
a) (m+1)^2>=4m
<=>(m+1)*(m+1)>=4m
=>m2+m+m2+m>=4m
=>2m2+2m>=4m
=>2(m2+m)>=4m
xét m=0=>2(02+0)=4*0
=>2(m2+m)=4m (1)
xét m\(\ne\)0 vì m2+m=4m với mọi m
=>2(m2+m)>4m (2)
từ (1) và (2)=>(m+1)^2>=4m
1. Cho a;b thuộc tập hợp số nguyên. Chứng minh ( a-b ) và ( b-a ) là hai số đối
2. Chứng tỏ rằng:
a, (x-y) + (m-n) = (x+m) - (y+n)
b, (x-y) - (m-n) = (x+n) - (y+m)
1. ta có: (a-b) + (b-a) = a-b+b-a = 0
Vậy (a-b) và (b-a) là hai số đối nhau
2.
a, (x-y) + (m-n) = x-y +m - n = x + m - y - n = (x+m) - (y+n)
b, (x-y) - (m-n) = x-y -m +n = x+n -y -m = (x+n) -(y+m)
A + B = a - b + b - a
A + B= a + (-b) + b + (-a)
A + B= a + (-a) + b + (-b)
A + B = 0
Vì A + B = 0 mà hai số đối có tổng = 0 nên a - b và b - a là hai số đối nhau.
a) (x - y) + (m - n)= x - y + m - n
= x + (-y) + m + (-n)
= (x + m) + (-y) + (-n)
= (x + m) +[- (y + n)]
= (x + m) - (y + n)
b) (x - y) - (m - n)= x - y - m + n
= x + (-y) + (-m) + n
= (x + n) + (-y) + (-m)
= (x + n) + [- (y + m)]
= (x + n) - (y + m)
A + B = a - b + b - a
A + B= a + (-b) + b + (-a)
A + B= a + (-a) + b + (-b)
A + B = 0
Vì A + B = 0 mà hai số đối có tổng = 0 nên a - b và b - a là hai số đối nhau.
a) (x - y) + (m - n)= x - y + m - n
= x + (-y) + m + (-n)
= (x + m) + (-y) + (-n)
= (x + m) +[- (y + n)]
= (x + m) - (y + n)
b) (x - y) - (m - n)= x - y - m + n
= x + (-y) + (-m) + n
= (x + n) + (-y) + (-m)
= (x + n) + [- (y + m)]
= (x + n) - (y + m)